练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】□ABCD中，∠A＝60°，则∠B的度数为（ ）

    A. 30° B. 45° C. 60° D. 120°

    【答案】D

    【解析】解决问题时根据题目所给的已知条件，利用平行四边形的性质：平行四边形的对角相等即可求出∠C的度数.

    ∵四边形ABCD是平行四边形，∴∠B+∠A=180°，∴∠B=180°-60°=120°,

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一个锐角的余角加上90°，就等于( )
    A.这个锐角的余角
    B.这个锐角的补角
    C.这个锐角的2倍
    D.这个锐角的3倍

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】6月5日是世界环境日，某校组织了一次环保知识竞赛，每班选25名同学参加比赛，成绩分别为A、B、C、D四个等级，其中相应等级的得分依次记为100分、90分、80分、70分，学校将某年级的一班和二班的成绩整理并绘制成统计图．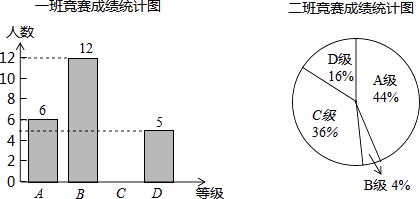

    平均数（分）

    中位数（分）

    众数（分）

    一班

    a

    b

    90

    二班

    d

    80

    c


    （1）把一班竞赛成绩统计图补充完整；
    （2）写出表中a、b、c的值：

    平均数（分）

    中位数（分）

    众数（分）

    一班

    a

    b

    90

    二班

    d

    80

    c


    （3）请从平均数和中位数方面比较一班和二班的成绩，对这次竞赛成绩的结果进行分析．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有理数的计算

    ① ②

    ③ ④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，点E，F在BC上，BE=CF,∠A=∠D，∠B=∠C,AF与DE交于点O .

    （1）求证：AB=DC;

    （2）求证：△OEF是等腰三角形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

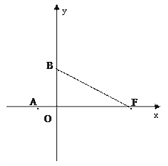
    【题目】已知抛物线经过点A（-3， 0）,F（8， 0）,B（0， 4）三点.

    （1）求抛物线解析式及对称轴.

    （2）若点D在线段FB上运动（不与F,B重合），过点D作DC⊥轴于点C（x, 0），将△FCD沿CD向左翻折，点B对应点为点E, △CDE与△FBO重叠部分面积为S.

    ①试求出S与x之间的函数关系式，并写出自变量取值范围.

    ②是否存在这样的点C，使得△BDE为直角三角形，若存在，求出C点坐标，若不存在，请说明理由；

    （3）抛物线对称轴上有一点M,平面内有一点N,若以A,B,M,N四点组成的四边形为菱形，求点N的坐标；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝ax2+bx+c中，函数y与自变量x的部分对应值如表，

    x

    6.17

    6.18

    6.19

    6.20

    y

    ﹣0.03

    ﹣0.01

    0.02

    0.04

    则方程ax2+bx+c＝0的一个解的范围是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法错误的是（ ）．
    A.两个互余的角都是锐角;
    B.一个角的补角大于这个角本身;
    C.互为补角的两个角不可能都是锐角;
    D.互为补角的两个角不可能都是钝角

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O的直径，点D，E为⊙O上的两个点，延长AD至C，使∠CBD=∠BED.

    （1）求证：BC是⊙O的切线；

    （2）当点E为弧AD的中点且∠BED=30°时，⊙O半径为2，求DF的长度.

    查看答案和解析>>

    同步练习册答案