
如图,已知:△ABC中,
(1)只用直尺(没有刻度)和圆规求作一点P,使点P同时满足下列两个条件(保留作图痕迹,不必写出作法):①点P到∠CAB的两边距离相等:②点P到A,B两点的距离相等。
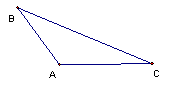
(2)若△ABC中,AC = AB = 4,∠CAB=120°,那么请计算以△ABC为轴截面的圆锥的侧面积(保留根号和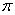 )。
)。
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
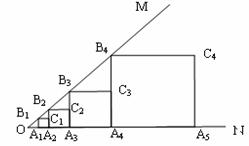
∠MON=45º,OA1=1,作正方形A1B1C1A2,面积记作S1;再作第二个正方形A2B2C2A3,面积记作S2;继续作第三个正方形A3B3C3A4,面积记作S3;点A1、A2、A3、A4……在射线ON上,点B1、B2、B3、B4……在射线OM上,……依此类推,则第6个正方形的面积S6是
查看答案和解析>>
科目:初中数学 来源: 题型:
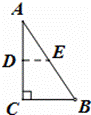
如图,直角三角形纸片ABC的∠C为90°,将三角形纸片沿着图示的中位线DE剪开,然后把剪开的两部分重新拼接成不重叠的图形,下列选项中不能拼出的图形是( )
A.直角梯形 B.矩形 C.等腰梯形 D.平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
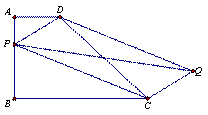
已知梯形ABCD, AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,问题:
(1)如图1,P为AB边上一点,以PD、PC为边做平行四边形PCQD,请问对角线PQ,DC的长能否相等,为什么?
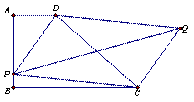
(2)如图2,P为AB边上任意一点,以PD、PC为边做平行四边形PCQD,请问对角线PQ的长是否存在最小值?若果存在,请求出最小值;如果不存在,请说明理由。
(3)P为AB边上任意一点,延长PD到E,使DE=PD,以PE、PC为边做平行四边形PCQE,请探究对角线PQ的长是否也存在最小值?若果存在,请求出最小值;如果不存在,请说明理由。
(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
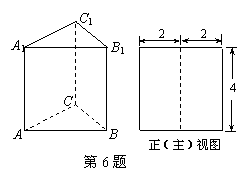
如图,三棱柱 的侧棱长和底面边长均为4,且侧棱
的侧棱长和底面边长均为4,且侧棱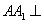 底面
底面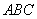 ,其正(主)视图是边长为4的正方形,则此三棱柱侧(左)视图的面积为( )
,其正(主)视图是边长为4的正方形,则此三棱柱侧(左)视图的面积为( )
A.4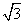 B.
B.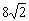 C.
C.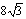 D.8
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
|
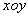 中,A、B两点的坐标分别为A(2,4),B(a,-4)(其中a>0),∠AOB=90°,点C在
中,A、B两点的坐标分别为A(2,4),B(a,-4)(其中a>0),∠AOB=90°,点C在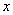 轴的正半轴上.动点P从点O出发,在四边形OACB的边上依次沿O→A→C→B向点B移动,当点P与点B重合时停止运动.设点P移动的路径的长为
轴的正半轴上.动点P从点O出发,在四边形OACB的边上依次沿O→A→C→B向点B移动,当点P与点B重合时停止运动.设点P移动的路径的长为 ,△POB的面积为
,△POB的面积为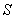 ,
,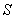 与
与 的函数关系的图象如图2所示,其中四边形ODEF是梯形.
的函数关系的图象如图2所示,其中四边形ODEF是梯形. (1)结合以上信息及图2填空:图2中的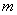 = ;
= ;
(2)求B,C两点的坐标及图2中OF的长;
(3)在图1中,当动点P恰为经过O、C两点的抛物线的顶点时,
①求此抛物线的解析式;
②若点Q在抛物线上,满足以C、P、Q三点为顶点的三角形是直角三角形,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
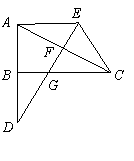
已知:如图,在直角△ABC中,∠ABC=90°,延长AB至点D,使AD=AC,取AC的中点为F,连DF交BC于点G,并延长至点E,使AE=CE.
(1)求证:⊿ABC≌⊿ADF;
(2)求证: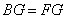 .(改编)
.(改编)
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com