
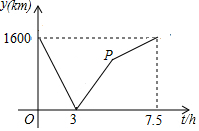
 A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示.
A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示.分析 (1)根据图中信息即可得到两车的速度;
(2)根据题意和图形即可得到点P的坐标以及点P表示的实际意义;
(3)根据题意,利用分类讨论的数学思想可以解答本题.
解答 解:(1)动车甲的速度=$\frac{1600}{7.5}$=$\frac{640}{3}$km/h,动车乙的速度,=$\frac{1600-\frac{640}{3}×3}{3}$=320km/h;
(2)由题意可得,
点P的横坐标为:1600÷320=5,纵坐标为:$\frac{640}{3}×5$=$\frac{3200}{3}$,
即点P的坐标为(5,$\frac{3200}{3}$),
该点坐标表示的实际意义是此时动车乙到达目的地,动车甲鱼动车乙的距离为$\frac{3200}{3}$km;
(3)由题意可得,
当相遇前相遇1200km,此时的时间为:$\frac{1600-1200}{\frac{640}{3}+320}$=0.75h,
当相遇后相遇1200km,由(2)知,当动车乙到达目的地时两车相距$\frac{3200}{3}<1200$,
故此时的时间为:$\frac{1200}{\frac{640}{3}}=\frac{45}{8}$h,
即两车在0.75h和$\frac{45}{8}$h相距1200km.
点评 本题考查了一次函数应用中的相遇问题,解题的关键是明确题意,利用数形结合的思想和分类讨论的数学思想解答.


科目:初中数学 来源: 题型:填空题
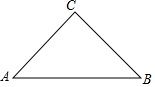
 如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是3$\sqrt{2}$cm.
如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是3$\sqrt{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠C=90°,CA=CB=4,将△ABC翻折,使得点B与边AC的中点M重合,如果折痕与边AB的交点为E,那么BE的长为$\frac{5\sqrt{2}}{3}$.
如图,在Rt△ABC中,∠C=90°,CA=CB=4,将△ABC翻折,使得点B与边AC的中点M重合,如果折痕与边AB的交点为E,那么BE的长为$\frac{5\sqrt{2}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
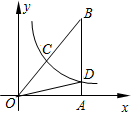 如图,已知反比例函数y=$\frac{k}{x}$(k>0)的图象经过Rt△OAB斜边OB的中点C,且与直角边AB相交于点D,若B的坐标为(4,6),则△BOD的面积为9.
如图,已知反比例函数y=$\frac{k}{x}$(k>0)的图象经过Rt△OAB斜边OB的中点C,且与直角边AB相交于点D,若B的坐标为(4,6),则△BOD的面积为9.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>-7 | B. | k≥-7 | C. | k≥0 | D. | k≥1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
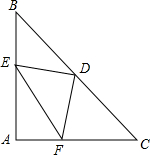 如图,在△ABC中,AB=AC,∠A=90°,点D是BC边的中点,点E,F分别在AB,AC上.且DE⊥DF.
如图,在△ABC中,AB=AC,∠A=90°,点D是BC边的中点,点E,F分别在AB,AC上.且DE⊥DF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com