
分析 (1)在Rt△ABO中,根据OB=4,∠BAO=30°解直角三角形即可.
(2)如图1中,作CM⊥AB于M,DN⊥OB于M.求出直线AB的解析式为y=$\sqrt{3}$x+4$\sqrt{3}$,设E(t,$\sqrt{3}$t+4$\sqrt{3}$),由△CEM≌△DCN,推出DN=CM,CN=EM,由BC=2,E(t,$\sqrt{3}$t+4$\sqrt{3}$),推出BM=1,BE=-8-2t,EM=-7-2t,推出CN=BM=-7-2t,推出ON=-5-2t,即可解决问题.
(3)分两种情形①如图2中,当点F在AB上时,利用中点坐标公式由C(-2,0),D(2t+5,$\sqrt{3}$),E(t,$\sqrt{3}$t+4$\sqrt{3}$),推出E关于CD的对称点F点的坐标为(t+3,-3$\sqrt{3}$-$\sqrt{3}$t),推出tan∠FOB=$\frac{-3\sqrt{3}-\sqrt{3}t}{-t-3}$=$\sqrt{3}$,推出∠FOB=60°,由∠FBO=60°,推出△FBO是等边三角形,由此即可解决问题.②如图3中,当OF=OB时,先求出点F坐标,列出方程求出t即可.
解答 解:(1)∵B(-4,0),
∴OB=4,
在Rt△AOB中,∵∠AOB=90°,∠BAO=30°,OB=4,
∴AB=2OB=8.
(2)如图1中,作CM⊥AB于M,DN⊥OB于M.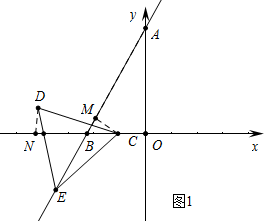
∵A(0,4$\sqrt{3}$),B(-4,0),
∴直线AB的解析式为y=$\sqrt{3}$x+4$\sqrt{3}$,设E(t,$\sqrt{3}$t+4$\sqrt{3}$),
∵∠DCE=∠ABC=60°,
∴∠DCN+∠BCE=∠BCE+∠CEM,
∴∠CEM=∠DCN,
在△CEM和△DCN中,
$\left\{\begin{array}{l}{∠CME=∠DNC}\\{∠CEM=∠DCN}\\{CE=CD}\end{array}\right.$,
∴△CEM≌△DCN,
∴DN=CM,CN=EM,
∵BC=2,E(t,$\sqrt{3}$t+4$\sqrt{3}$),
∴BM=1,BE=-8-2t,EM=-7-2t,
∴CN=BM=-7-2t,
∴ON=-5-2t,
∴点D坐标(2t+5,$\sqrt{3}$),
∴D点横坐标d=2t+5,
(3)①如图2中,当点F在AB上时,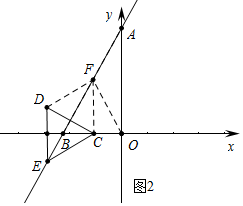
∵C(-2,0),D(2t+5,$\sqrt{3}$),E(t,$\sqrt{3}$t+4$\sqrt{3}$),
∴E关于CD的对称点F点的坐标为(t+3,-3$\sqrt{3}$-$\sqrt{3}$t),
∴tan∠FOB=$\frac{-3\sqrt{3}-\sqrt{3}t}{-t-3}$=$\sqrt{3}$,
∴∠FOB=60°,∵∠FBO=60°,
∴△FBO是等边三角形,
∴F(-2,2$\sqrt{3}$),
∴t+3=-2,
∴t=-5,
∴d=2t+5=-5.
②如图3中,当OF=OB时,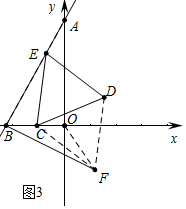
由①可知∠BOF=120°,
∵OB=OF=4,
∴F(2,2$\sqrt{3}$),
∴t+3=2,
∴t=-1,
∴d=2t+5=3.
综上所述,当△OBF为等腰三角形时d的值为-5或3.
点评 本题考查几何变换综合题、等边三角形的性质、一次函数、锐角三角函数、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,本题体现了数形结合的数学思想,利用中点坐标公式求出点F坐标,发现特殊角,是解题的突破口,属于中考压轴题.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{12}{13}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
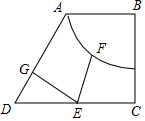 如图,直角梯形ABCD中,AB∥DC,∠B=90°,AB=1,BC=2,CD=3,以B为圆心,半径为1的弧交BC于M,E是线段CD上一动点,EG⊥AD,垂足为G,F是弧AM上一动点,则EG+EF的最小值为$\frac{5\sqrt{2}-2}{2}$.
如图,直角梯形ABCD中,AB∥DC,∠B=90°,AB=1,BC=2,CD=3,以B为圆心,半径为1的弧交BC于M,E是线段CD上一动点,EG⊥AD,垂足为G,F是弧AM上一动点,则EG+EF的最小值为$\frac{5\sqrt{2}-2}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷(解析版) 题型:解答题
何老师安排喜欢探究问题的小明解决某个问题前,先让小明看了一个有解答过程的例题.
例:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
【解析】
∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0∴m=﹣3,n=3
为什么要对2n2进行了拆项呢?
聪明的小明理解了例题解决问题的方法,很快解决了下面两个问题.相信你也能很好的解决下面的这两个问题,请写出你的解题过程..
解决问题:
(1)若x2﹣4xy+5y2+2y+1=0,求xy的值;
(2)已知a、b、c是△ABC的三边长,满足a2+b2=10a+12b﹣61,c是△ABC中最短边的边长,且c为整数,那么c可能是哪几个数?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com