
在平面直角坐标系xoy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,
给出如下定义:
若∣x1-x2∣≥∣y1-y2∣,则点P1与点P2的“非常距离”为∣x1-x2∣;
若∣x1-x2∣<∣y1-y2∣,则点P1与点P2的“非常距离”为∣y1-y2∣.
例如:点P1(1,2),点P2(3,5),因为∣1-3∣<∣2-5∣,所以点P1与点P2的“非常距离”为
∣2-5∣=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x
轴的直线P2Q的交点)。
(1)已知点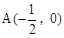 ,B为y轴上的一个动点,
,B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值;
(2)已知C是直线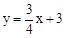 上的一个动点,
上的一个动点,
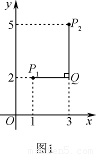
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最
小值及相应的点E和点C的坐标。
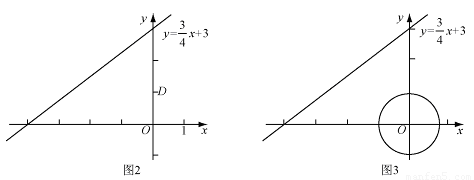
解:(1)①(0,-2)或(0,2)。
② 。
。
(2)①设C坐标为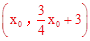 ,如图,过点C作CP⊥x轴于点P,作CQ⊥y轴于点Q。
,如图,过点C作CP⊥x轴于点P,作CQ⊥y轴于点Q。
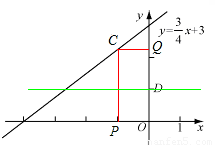
由“非常距离”的定义知,当OP=DQ时,点C与点D的“非常距离”最小,
∴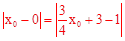 。
。
两边平方并整理,得 ,解得,
,解得,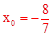 或
或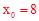 (大于
(大于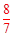 ,舍去)。
,舍去)。
∴点C与点D的“非常距离”的最小值距离为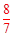 ,此时
,此时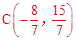 。
。
②设直线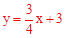 与x轴和y轴交于点A,B,过点O作直线
与x轴和y轴交于点A,B,过点O作直线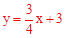 的垂线交直线
的垂线交直线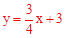 于点C,交圆于点E,过点C作CP⊥x轴于点P,作CQ⊥y轴于点Q,过点E作EM⊥x轴于点M,作EN⊥y轴于点N。
于点C,交圆于点E,过点C作CP⊥x轴于点P,作CQ⊥y轴于点Q,过点E作EM⊥x轴于点M,作EN⊥y轴于点N。
易得,OA=4,OB=3,AB=5。
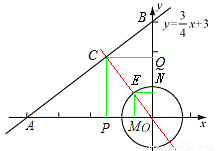
由△OAB∽△MEM,OE=1,得OM=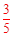 ,ON=
,ON=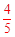 。∴
。∴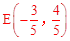 。
。
设C坐标为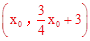
由“非常距离”的定义知,当MP=NQ时,点C与点E的“非常距离”最小,
∴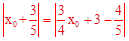 。
。
两边平方并整理,得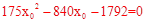 ,
,
解得,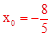 或
或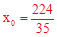 (大于
(大于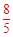 ,舍去)。
,舍去)。
∴点C与点E的“非常距离”的最小值距离为1,此时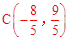 ,
,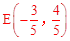 。
。
【解析】新定义,直线上点的坐标与方程的关系,直线和圆的性质,解一元二次方程,勾股定理,相似三角形的和性质。
(1)根据“非常距离”的定义可直接求出。
(2)①解题关键是,过C点向x、y轴作垂线,当CP和CQ长度相等的时候“非常距离”最短,理由是,如果向下(如左图)或向上(如右图)移动C点到达C’点,其与点D的“非常距离”都会增大。故而C、D为正方形相对的两个顶点时有最小的非常距离。
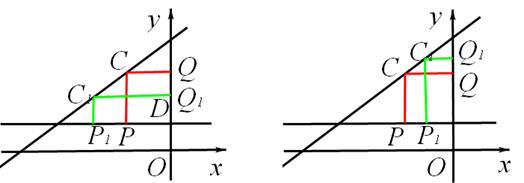
②同①,同时理解当OC垂直于直线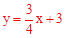 时,点C与点E的“非常距离”最小。
时,点C与点E的“非常距离”最小。


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com