练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下面的多项式中，能因式分解的是( )

    A. m2+n2B. m2+4m+1C. m2-nD. m2-2m+1

    【答案】D

    【解析】

    根据因式分解是把一个多项式化成几个整式乘积的形式，可得答案．

    A、B、C三项没有公因式，也不能用 公式法进行因式分解，故错误；

    D、m2-2m+1=（m-1）2

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】问题背景:

    如图（a）,点A、B在直线l的同侧，要在直线l上找一点C，使AC与BC的距离之和最小，我们可以作出点B关于l的对称点B′,连接A B′与直线l交于点C，则点C即为所求.

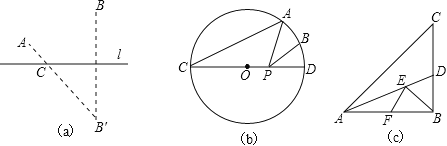
    （1）实践运用：

    如图(b)，已知，⊙O的直径CD为4，点A 在⊙O 上，∠ACD=30°，B 为弧AD 的中点，P为直径CD上一动点，则BP+AP的最小值为 ．

    （2）知识拓展：

    如图(c)，在Rt△ABC中，AB=10，∠BAC=45°，∠BAC的平分线交BC于点D，E、F分别是线段AD和AB上的动点，求BE+EF的最小值，并写出解答过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点P（3，﹣2）关于y轴的对称点是 ， 关于原点的对称点是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列语句：①全等三角形的周长相等．②面积相等的三角形是全等三角形．③若成轴对称的两个图形中的对称线段所在直线相交，则这个交点一定在对称轴上．④全等三角形的所有边相等．其中正确的有（　　）

    A. 0个 B. 1个 C. 2个 D. 3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】探索与研究：
    方法1：如图（a），对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得，所以
    ∠BAE＝90°，且四边形ACFD是一个正方形，它的面积和四边形ABFE面积相等，而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和，根据图示写出证明勾股定理的过程；

    方法2：如图（b），是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的，你能根据图示再写一种证明勾股定理的方法吗？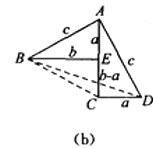

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各式计算结果正确的是（ ）
    A.a+a=a2
    B.（a﹣1）2=a2﹣1
    C.aa=a2
    D.（3a）3=9a2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】羊年除夕当日微信红包收发总量达80.8亿个．其中80.8亿用科学记数法可表示为（ ）
    A.8.08×108
    B.0.808×109
    C.8.08×109
    D.0.808×1010

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在△ABC中，∠BAC=90°，AB⊥AC，AB=3，BC=5，EF垂直平分BC，点P为直线EF上的任一点，则AP+BP的最小值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】元月份某天某市的最高气温是4℃，最低气温是-5℃，那么这天的温差（最高气温减最低气温）是______℃．

    查看答案和解析>>

    同步练习册答案