
| A. | k>-7 | B. | k≥-7 | C. | k≥0 | D. | k≥1 |
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
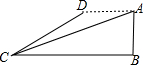 如图,飞机的高度AB=1000千米,从飞机上测得地面着陆点C的俯角为18°,飞机水平飞行一段距离后,到达D点,此时测得地面着陆点C的俯角为30°,求飞机飞行的距离AD的长(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,tan18°≈0.32)
如图,飞机的高度AB=1000千米,从飞机上测得地面着陆点C的俯角为18°,飞机水平飞行一段距离后,到达D点,此时测得地面着陆点C的俯角为30°,求飞机飞行的距离AD的长(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,tan18°≈0.32)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
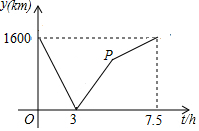 A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示.
A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
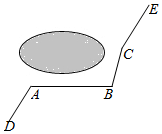 如图所示,一条公路修到湖边时,为了保护生态环境,需拐弯绕湖而过,如果图中的拐角∠A=150°,∠B=120°,三次拐弯后的道路CE与原来公路DA平行,试求出∠C的度数.
如图所示,一条公路修到湖边时,为了保护生态环境,需拐弯绕湖而过,如果图中的拐角∠A=150°,∠B=120°,三次拐弯后的道路CE与原来公路DA平行,试求出∠C的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com