
| A. | 平面上三个点确定一个圆 | |
| B. | 与某圆一条半径垂直的直线是该圆的切线 | |
| C. | 三角形的外心在三角形的外面 | |
| D. | 等弧所对的圆周角相等 |
分析 根据确定圆的条件对A进行判断;根据切线的判定定理对B进行判断;根据三角形的外心定义对C进行判断;根据圆周角定理对D进行判断.
解答 解:A、平面上不共线的三点确定一个圆,所以A选项错误;
B、过圆的半径的外端点与此半径垂直的直线是该圆的切线,所以B选项错误;
C、钝角三角形的外心在三角形外部,锐角三角形的外心在三角形内部,直角三角形的外心在斜边的中点,所以C选项错误;
D、等弧所对的圆周角相等,所以D选项正确.
故选D.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.


科目:初中数学 来源: 题型:解答题
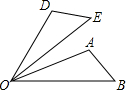 如图,△AOB绕点O旋转到△DOE的位置,请指出旋转角.
如图,△AOB绕点O旋转到△DOE的位置,请指出旋转角.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 输入数据 | 1 | 2 | 3 | 4 | 5 | … |
| 输出数据 | $\frac{2}{3}$ | $\frac{4}{5}$ | $\frac{6}{7}$ | $\frac{8}{9}$ | $\frac{10}{11}$ | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在4×4的正方形网格中,则tanα的值是( )
如图,在4×4的正方形网格中,则tanα的值是( )| A. | 1 | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com