若Rt△ABC中，∠C=90°，c=5，b=3，则△ABC的内切圆的半径r=________．
1
分析：如图：由Rt△ABC中，∠C=90°，c=5，b=3，可得a=4；又因为⊙O为△ABC的内切圆，所以AE=AD，CE=CF，BD=BF；易证四边形OECF是正方形，则列方程即可求得⊙O的半径r．
解答：
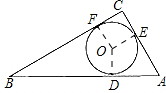
解：∵Rt△ABC中，∠C=90°，c=5，b=3，
∴a=4，
∵⊙O为△ABC的内切圆，
∴AE=AD，CE=CF，BD=BF，OE⊥AC，OF⊥BC，
∴∠OFC=∠OEC=∠C=90°，
∴四边形OECF是矩形；
∵OE=OF，
∴四边形OECF是正方形；
∵⊙O的半径为r，
∴CE=CF=r，AE=AD=3-r，BD=BF=4-r，
∴3-r+4-r=5，
∴r=1，
∴△ABC的内切圆的半径r=1．
点评：此题考查了三角形内切圆的性质．注意切线长定理，还要注意直角三角形的内切圆中，如果连接过切点的半径，可以得到一个正方形，借助于方程即可求得半径的长．
