

 =
= ,试求x.
,试求x.
 即可求得∠COE的度数,从而得到∠DOE、∠BOE的度数,即可求得结果.
即可求得∠COE的度数,从而得到∠DOE、∠BOE的度数,即可求得结果.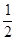 ∠AOC=70°
∠AOC=70°
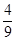 ×90°=40°
×90°=40° 

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源:不详 题型:解答题
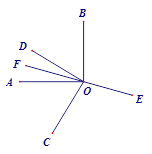
 °,
°, °,
°, ;
; 平分∠BOC,
平分∠BOC,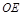 平分∠AOC,直接写出∠DOE的度数为 °;
平分∠AOC,直接写出∠DOE的度数为 °; °改成
°改成 ,其他条件不变,你能求出∠DOE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
,其他条件不变,你能求出∠DOE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.0个 | B.1个 | C.2个 | D.3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com