
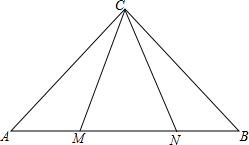
 如图所示,等腰直角△ABC中,M、N为斜边AB上两点,且∠MCN=45°,求证:以AM、MN、BN三边为边长构成的三角形是直角三角形.
如图所示,等腰直角△ABC中,M、N为斜边AB上两点,且∠MCN=45°,求证:以AM、MN、BN三边为边长构成的三角形是直角三角形. 分析 把△ACN绕C点逆时针旋转45°,得△CBD,这样∠ACM+∠BCN=45°就集中成一个与∠MCN相等的角,在一条直线上的AM、MN、NB集中为△DNB,只需判定△DNB的形状即可.
解答 证明:设:AM=m,MN=n,NB=k,
如图:作△ACM≌△BCD,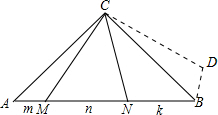
∴∠ACM=∠BCD,CM=CD,∠MCN=∠NCD=45°,
又∵CN=CN,
∴△MNC≌△DNC,MN=ND,AM=BD=m,
又∵∠DBN=45°+45°=90°,
∴n2=m2+k2.
∴以AM、MN、BN三边为边长构成的三角形是直角三角形.
点评 本题考查等腰直角三角形的性质,难度较大,注意掌握旋下列情形常实施旋转变换:(1)图形中出现等边三角形或正方形,把旋转角分别定为60°、90°;(2)图形中有线段的中点,将图形绕中点旋转180°,构造中心对称全等三角形;(3)图形中出现有公共端点的线段,将含有相等线段的图形绕公共端点,旋转两相等线段的夹角后与另一相等线段重合.


科目:初中数学 来源: 题型:选择题
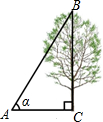 如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为( )米.
如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为( )米.| A. | 7tanα | B. | $\frac{7}{tanα}$ | C. | 7sinα | D. | 7cosα |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
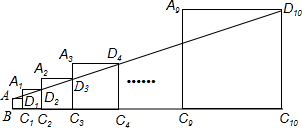 已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推….若A1C1=2,且点A,D2,D3,…,D10都在同一直线上,则正方形A9C9C10D10的边长是$\frac{{3}^{8}}{{2}^{7}}$.
已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推….若A1C1=2,且点A,D2,D3,…,D10都在同一直线上,则正方形A9C9C10D10的边长是$\frac{{3}^{8}}{{2}^{7}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
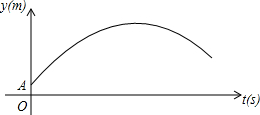 如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,将含30°的三角尺的直角顶点C落在第二象限.其斜边两端点A、B分别落在x轴、y轴上,且AB=12cm
如图,平面直角坐标系中,将含30°的三角尺的直角顶点C落在第二象限.其斜边两端点A、B分别落在x轴、y轴上,且AB=12cm查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com