
【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为x=1,经过点(-1,0),有下列结论:①abc<0;②a+c>b;③3a+c=0;④a+b>m(am+b)(其中m≠1)其中正确的结论有( )
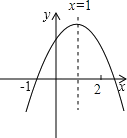
A. 1个
B. 2个
C. 3个
D. 4个
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】绿色植物销售公司打算销售某品种的“赏叶植物”,在针对这种“赏叶植物”进行市场调查后,绘制了以下两张函数图象.其中图①为一条直线,图②为一条抛物线,且抛物线顶点为(6,1),请根据图象解答下列问题:
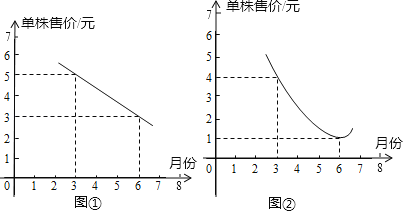
(1)如果公司在3月份销售这种“赏叶植物”,单株获利多少元;
(2)请直接写出图象①中直线的解析式;
(3)请你求出公司在哪个月销售这种“赏叶植物”,单株获利最大?(备注:单株获利=单株售价﹣单株成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线C1的图象与x轴交A(﹣3,0),B(1,0)两点,与y轴交于点C(0,3)点D为抛物线的顶点.
(1)求抛物线C1的解析式;
(2)将抛物线C1关于直线x=1对称后的抛物线记为C2,将抛物线C1关于点B对称后的抛物线记为C3,点E为抛物线C3的顶点,在抛物线C2的对称轴上是否存在点F,使得△BEF为等腰三角形?若存在请求出点F的坐标,若不存在请说明理由.
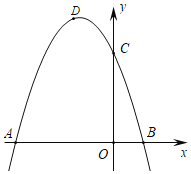
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公司为了运输的方便,将生产的产品打包成件,运往同一目的地.其中A产品和B产品共320件,A产品比B产品多80件.
(1)求打包成件的A产品和B产品各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批产品全部运往同一目的地.已知甲种货车最多可装A产品40件和B产品10件,乙种货车最多可装A产品和B产品各20件.如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.则公司安排甲、乙两种货车时有几种方案?并说明公司选择哪种方案可使运输费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,点A坐标为(2,0),点C坐标为(0,4).点P从点O出发,沿OA以每秒1个单位长度的速度向点A运动,同时点Q从点A出发,沿AB以每秒2个单位长度的速度向点B运动,当点P与点A重合时运动停止.设运动时间为t秒.
(1)当△CBQ与△PAQ相似时,求出t的值;
(2)当t=1时,抛物线y=2x2+bx+c经过P,Q两点,与y轴交于点M,在该抛物线上找点D,使∠MQD=![]() ∠MPQ,求点D的坐标.
∠MPQ,求点D的坐标.
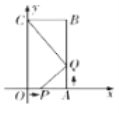
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的位置如图所示.

(1)分别写出△ABC各个顶点的坐标;
(2)分别写出顶点A关于x轴对称的点A′的坐标、顶点B关于y轴对称的点B′的坐标及顶点C关于原点对称的点C′的坐标;
(3)求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数![]() (x>0)与正比例函数y=kx、
(x>0)与正比例函数y=kx、 ![]() (k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
(k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
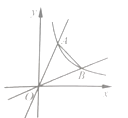
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为方便住校生晚自习后回到宿舍就寝,新安装了一批照明路灯;一天上午小刚在观看新安的照明灯时,发现在太阳光的正面照射下,照明灯的灯杆的投影的末端恰好落在2.5米高文化走廊墙的顶端,小刚测得照明灯的灯杆的在太阳光下的投影从灯杆的杆脚到文化走廊的墙脚的影长为4.6米,同一时刻另外一个前来观看照明路灯小静测得身高1.5米小刚站立时在太阳光下的影长恰好为1米,请同学们画出与问题相关联的线条示意图并求出新安装的照明路灯的灯杆的高度?
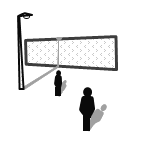
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小雪设计的“作以已知线段为斜边的等腰直角三角形”的尺规作图过程.
![]()
已知:线段AB.
求作:以AB为斜边的一个等腰直角△ABC.
作法:
(1)分别以点A和点B为圆心,大于![]() AB的长为半径作弧,两弧相交于P、Q两点;
AB的长为半径作弧,两弧相交于P、Q两点;
(2)作直线PQ,交AB于点O;
(3)以O为圆心,OA的长为半径作圆,交直线PQ于点C;
(4)连接AC,BC.
则△ABC即为所求作的三角形.根据小雪设计的尺规作图过程:
(1)使用直尺和圆规补全图形(保留作图痕迹);
(2)完成下面的证明:
证明:∵PA=PB,QA=QB,∴PQ垂直平分AB( )
在⊙O中,
∵AB为直径,∴∠ACB=90°( )
又∵∠AOC=∠BOC=90°,∴AC=BC( ),∴△ABC为以AB为斜边的等腰直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com