
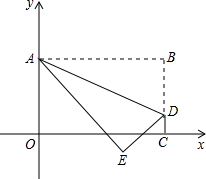
 将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.分析 (1)根据点A、点D、点C的坐标和矩形的性质可以得到点B和点E的坐标;
(2)由折叠的性质求得线段DE和AE的长,然后利用勾股定理得到有关m的方程,求得m的值即可;
(3)过点E作EF⊥AB于F,EF分别与 AD、OC交于点G、H,过点D作DP⊥EF于点P,首先利用勾股定理求得线段DP的长,从而求得线段BF的长,再利用△AFG∽△ABD得到比例线段求得线段FG的长,最后求得a的取值范围.
解答 解:(1)点B的坐标为(3,4),
∵AB=BD=3,
∴△ABD是等腰直角三角形,
∴∠BAD=45°,
则∠DAE=∠BAD=45°,
则E在y轴上.
AE=AB=BD=3,
∴四边形ABDE是正方形,OE=1,
则点E的坐标为(0,1);
故答案为(3,4),(0,1);
(2)点E能恰好落在x轴上.理由如下:
∵四边形OABC为矩形,
∴BC=OA=4,∠AOC=∠DCE=90°,
由折叠的性质可得:DE=BD=OA-CD=4-1=3,AE=AB=OC=m,
如图1,假设点E恰好落在x轴上,在Rt△CDE中,由
勾股定理可得EC=$\sqrt{D{E}^{2}-C{D}^{2}}$=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$,
则有OE=OC-CE=m-2$\sqrt{2}$,
在Rt△AOE中,OA2+OE2=AE2
即42+(m-2$\sqrt{2}$)2=m2,解得m=3$\sqrt{2}$;
(3)如图,过点E作EF⊥AB于F,EF分别与AD、OC交于点G、H,过点D作DP⊥EF于点P,则EP=PH+EH=DC+EH=2,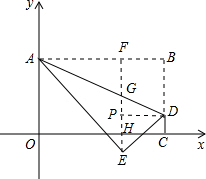
在Rt△PDE中,由勾股定理可得$\sqrt{D{E}^{2}-E{P}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,
∴BF=DP=$\sqrt{5}$,
在Rt△AEF中,AF=AB-BF=m-$\sqrt{5}$,EF=5,AE=m
∵AF2+EF2=AE2
∴(m-$\sqrt{5}$)2+52=m2,
解得m=3$\sqrt{5}$,
∴AAB=3$\sqrt{5}$,AF=2$\sqrt{5}$,E(2$\sqrt{5}$,-1)
∵∠AFG=∠ABD=90°,∠FAG=∠BAD
∴△AFG∽△ABD
∴$\frac{AF}{AB}$=$\frac{FG}{BD}$,即$\frac{2\sqrt{5}}{3\sqrt{5}}$=$\frac{FG}{3}$,
解得FG=2,
∴EG=EF-FG=3
∴点G的纵坐标为2,
∵点($2\sqrt{5}$,a)在直线x=2$\sqrt{5}$上,且点($2\sqrt{5}$,a)落在△ADE的内部,
∴此点必在EG上,
∴-1<a<2,
故a的取值范围为-1<a<2.
点评 本题考查了二次函数的综合知识,是一道有关折叠的问题,主要考查二次函数、矩形、相似形等知识,试题中贯穿了方程思想和数形结合的思想,请注意体会.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
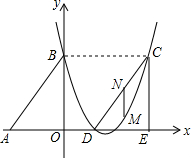 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}{x}^{2}+bx+c$经过B点,且顶点在直线x=$\frac{5}{2}$上.
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}{x}^{2}+bx+c$经过B点,且顶点在直线x=$\frac{5}{2}$上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 480×108元 | B. | 4.8×1010元 | C. | 4.80×1010元 | D. | 4.80××108元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com