
科目:初中数学 来源: 题型:解答题
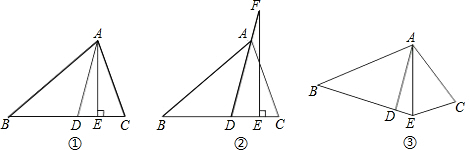
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 车辆随机到达一个路口,遇到红灯 | B. | 同位角相等,两条直线平行 | ||
| C. | 平行于同一条直线的两条直线平行 | D. | 对顶角相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
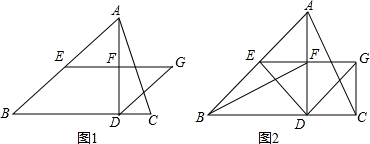
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
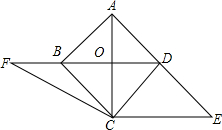 如图,已知正方形ABCD的对角线AC、BD交于点O,CE⊥AC与AD边的延长线交于点E.
如图,已知正方形ABCD的对角线AC、BD交于点O,CE⊥AC与AD边的延长线交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
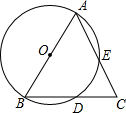 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D、E.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D、E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com