
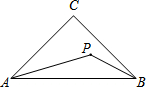
 如图,在△ABC中,∠C=90°,AC=BC=1,P为△ABC内一个动点,∠PAB=∠PBC,则CP的最小值为$\sqrt{2}$-1.
如图,在△ABC中,∠C=90°,AC=BC=1,P为△ABC内一个动点,∠PAB=∠PBC,则CP的最小值为$\sqrt{2}$-1. 分析 首先求得∠APB=135°,点P在以AB为弦的⊙O上,然后可求得OC=$\sqrt{2}$,OP=1,当点O、P、C在一条直线上时,PC有最小值.
解答 解:如图所示: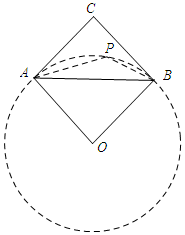
∵在△ABC中,∠C=90°,AC=BC=1,
∴∠CAB=∠CBA=45°.
又∵∠PAB=∠PBC,
∴∠PAB+∠PBA=45°.
∴∠APB=135°.
∴点P在以AB为弦的⊙O上.
∵∠APB=135°,
∴∠AOB=90°.
∴∠OAB=∠OBA=45°.
∴∠CAO=90°.
∴四边形ACBO为矩形.
∵OA=OB,
∴四边形AOBC为正方形.
∴OA=OB=1.
∴OP=1,OC=$\sqrt{2}$.
当点O、P、C在一条直线上时,PC有最小值,
∴PC的最小值=OC-OP=$\sqrt{2}$-1.
故答案为:$\sqrt{2}$-1.
点评 本题主要考查的是等腰直角三角形的性质、正方形的判定,证得点P在以AB为弦的圆弧上是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将?ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为( )
如图,将?ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为( )| A. | 124° | B. | 114° | C. | 104° | D. | 66° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC,∠A=30°,AC的垂直平分线分别交AB,AC于D,E.连接CD,若CD=1cm,则BD的长为( )
如图,在△ABC中,AB=AC,∠A=30°,AC的垂直平分线分别交AB,AC于D,E.连接CD,若CD=1cm,则BD的长为( )| A. | 1cm | B. | ($\sqrt{3}$-1)cm | C. | $\frac{\sqrt{3}}{2}$cm | D. | $\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
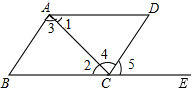 如图,四边形ABCD中,点E在BC延长线上,则下列条件中不能判断AB∥CD的是( )
如图,四边形ABCD中,点E在BC延长线上,则下列条件中不能判断AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠1=∠2 | C. | ∠5=∠ABC | D. | ∠1+∠3+∠D=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这种调查方式是抽样调查 | |
| B. | 每名学生的立定跳远成绩是个体 | |
| C. | 100名学生是样本容量 | |
| D. | 这100名学生的立定跳远成绩是总体的一个样本 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com