
 阅读材料,回答问题
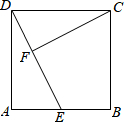
阅读材料,回答问题分析 (1)利用正方形是性质和平行线的性质,由“两角法”证明△ADE∽△FCD;
(2)根据相似三角形的对应边的比相等求解.
解答 解:(1)△ADE∽△FCD,理由如下:
∵四边形ABCD是正方形,
∴∠A=90°,AB∥CD,
∴∠CDF=∠DEA.
又CF⊥DE,
∴∠CFD=90°,即∠CFD=∠A,
因而,△ADE∽△FCD;
(2)由题意知,AD=CD=1,AE=$\frac{1}{2}$.
在直角△DEA中,有DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=$\sqrt{{1}^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{5}}{2}$.
由(1)可得:$\frac{CF}{AD}$=$\frac{CD}{DE}$,则CF=$\frac{AD•CD}{DE}$=$\frac{2\sqrt{5}}{5}$.
点评 本题考查了相似三角形的判定与性质,以及勾股定理的应用,正确证明△ADE∽△FCD是关键.


科目:初中数学 来源: 题型:解答题
| 销售量 | 单价 |
| 不超过100件的部分 | 2.5元/件 |
| 超过100件不超过300件的部分 | 2.2元/件 |
| 超过300件的部分 | 2元/件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
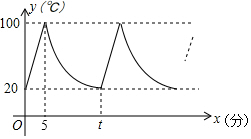 如图所示,小明家饮水机中原有水的温度是20℃,开机通电后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系.当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系.当水温降至20℃时,饮水机又自动开始加热…,不断重复上述程序.根据图中提供的信息,解答下列问题:
如图所示,小明家饮水机中原有水的温度是20℃,开机通电后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系.当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系.当水温降至20℃时,饮水机又自动开始加热…,不断重复上述程序.根据图中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 、(0,0 ) | B. | (1-$\sqrt{2}$,0)或($\sqrt{2}+$1,0) | C. | 、($\sqrt{2}$+1,0 ) | D. | 、(-$\sqrt{2}$-1,0)或(-$\sqrt{2}$+1,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com