
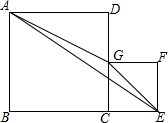
 如图,四边形ABCD与四边形CEFG是两个正方形,边长分别为a、b.其中B、C、E在一条直线上,G在线段CD上.三角形AGE的面积为S.
如图,四边形ABCD与四边形CEFG是两个正方形,边长分别为a、b.其中B、C、E在一条直线上,G在线段CD上.三角形AGE的面积为S.分析 (1)①根据S△AEG=S正方形ABCD+S正方形ECGF-S△ABE-S△ADG-S△EFG即可解决问题.
②方法同上.
(2)结论S=$\frac{1}{2}$b2.根据S△AEG=S正方形ABCD+S正方形ECGF-S△ABE-S△ADG-S△EFG即可证明.
解答  解:(1)①∵四边形ABCD与四边形CEFG是两个正方形,AB=5,EC=3,
解:(1)①∵四边形ABCD与四边形CEFG是两个正方形,AB=5,EC=3,
∴DG=CD-CG=5-3=2,
∴S△AEG=S正方形ABCD+S正方形ECGF-S△ABE-S△ADG-S△EFG
=25+9-$\frac{1}{2}$×8×5-$\frac{1}{2}$×5×2-$\frac{1}{2}$×3×3=4.5,
②)①∵四边形ABCD与四边形CEFG是两个正方形,AB=7,EC=3,
∴DG=CD-CG=7-3=4,
∴S△AEG=S正方形ABCD+S正方形ECGF-S△ABE-S△ADG-S△EFG
=49+9-$\frac{1}{2}$×10×7-$\frac{1}{2}$×7×4-$\frac{1}{2}$×3×3=4.5.
(2)结论S=$\frac{1}{2}$b2.
证明:∵S△AEG=S正方形ABCD+S正方形ECGF-S△ABE-S△ADG-S△EFG
=a2+b2-$\frac{1}{2}$(a+b)•a-$\frac{1}{2}$•a(a-b)-$\frac{1}{2}$b2
=a2+b2-$\frac{1}{2}$a2-$\frac{1}{2}$ab-$\frac{1}{2}$a2+$\frac{1}{2}$ab-$\frac{1}{2}$b2
=$\frac{1}{2}$b2.
∴S=$\frac{1}{2}$b2.
点评 本题考查四边形综合题、正方形的性质,解题的关键是学会利用分割法求三角形面积,注意善于发现规律,利用规律解决问题,善于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 平行四边形ABCD中,CD=8,∠C=60°,点P为边BC上一动点,连接DP,作∠ADP的平分线交CB的延长线于F.
平行四边形ABCD中,CD=8,∠C=60°,点P为边BC上一动点,连接DP,作∠ADP的平分线交CB的延长线于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,过象限内一点分别作坐标轴的垂线,若与坐标轴围成的矩形的周长与面积相等,则这个点叫做“和谐点”.如图,过点H(-3,6)分别作x轴,y轴的垂线,与坐标轴围成的矩形OAHB的周长与面积相等,则点H(3,6)是“和谐点”.
在平面直角坐标系xOy中,过象限内一点分别作坐标轴的垂线,若与坐标轴围成的矩形的周长与面积相等,则这个点叫做“和谐点”.如图,过点H(-3,6)分别作x轴,y轴的垂线,与坐标轴围成的矩形OAHB的周长与面积相等,则点H(3,6)是“和谐点”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在□ABCD中,点E、F分别是边AD、CD的中点,过点E、F的直线交BA、BC的延长线于点G、H,联结AC.
如图,已知在□ABCD中,点E、F分别是边AD、CD的中点,过点E、F的直线交BA、BC的延长线于点G、H,联结AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com