
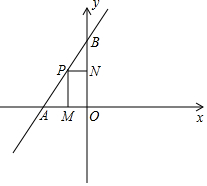
 如图,在平面直角坐标系中,直线y=$\frac{3}{2}$x+6与x轴交于点A,与y轴交于点B,P为线段AB上一动点(不与A,B两点重合),过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设OM=a,四边形PMON面积为s.
如图,在平面直角坐标系中,直线y=$\frac{3}{2}$x+6与x轴交于点A,与y轴交于点B,P为线段AB上一动点(不与A,B两点重合),过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设OM=a,四边形PMON面积为s.分析 (1)由直角解析式可求得A、B的坐标,由P在线段AB上运动,可知M在线段OA上运动,则可求得a的取值范围;
(2)用a可表示出PM和PN的长,则可求得s与a的函数表达式,利用二次函数的性质可求得其最大值;
(3)代入(2)中所求函数表达式,可求得对应的a的值,从而可求得P点坐标.
解答 解:
(1)在y=$\frac{3}{2}$x+6中,令y=0可求得x=-4,令x=0可求得y=6,
∴A(-4,0),B(0,6),
∵P为线段AB上一动点(不与A,B两点重合),过点P作PM⊥x轴,
∴点M在线段OA上运动,
∴0<a<4,
故答案为:(-4,0),(0,6);0<a<4;
(2)∵P为线段AB上一动点(不与A,B两点重合),PM⊥x轴,PN⊥y轴,且OM=a,
∴P(-a,-$\frac{3}{2}$a+6),
∴PM=-$\frac{3}{2}$a+6,
∵四边形PMON为矩形,
∴s=OM•PM=a(-$\frac{3}{2}$a+6)=-$\frac{3}{2}$a2+6a=-$\frac{3}{2}$(a-2)2+6,
∵-$\frac{3}{2}$<0,
∴当a=2时,s有最大值,最大值为6;
(3)当s=$\frac{35}{6}$时,则有$\frac{35}{6}$=-$\frac{3}{2}$a2+6a,解得a=$\frac{5}{3}$或a=$\frac{7}{3}$,
∴P点坐标为(-$\frac{5}{3}$,$\frac{17}{2}$)或(-$\frac{7}{3}$,$\frac{19}{2}$).
点评 本题为一次函数的综合应用,涉及函数图象与坐标轴的交点、矩形的面积、二次函数的性质等知识点.在(1)中注意函数图象与坐标轴的交点的求法,在(2)中用a表示出PM的长是解题的关键,在(3)中利用函数值即可求得对应的自变量a的值.本题考查知识点较多,综合性较强,但难度不大,较易得分.


科目:初中数学 来源: 题型:填空题
 阅读材料
阅读材料查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,平行四边形ABCD的对角线AC,BD相交于点O,补充下面一个条件,不能判定平行四边形ABCD是菱形的是( )
如图,平行四边形ABCD的对角线AC,BD相交于点O,补充下面一个条件,不能判定平行四边形ABCD是菱形的是( )| A. | AB=BC | B. | AO=BO | C. | ∠DOC=90° | D. | ∠CDO=∠ADO |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某衬衫厂生产某品牌衬衫的成本价为50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍.
某衬衫厂生产某品牌衬衫的成本价为50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点A是反比例函数y=$\frac{k}{x}$(k>0)图象第一象限上一点,过点A作AB⊥x轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,若S1-S2的值最大为1,则k的值为4$\sqrt{2}$+4.
如图,点A是反比例函数y=$\frac{k}{x}$(k>0)图象第一象限上一点,过点A作AB⊥x轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,若S1-S2的值最大为1,则k的值为4$\sqrt{2}$+4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 应试者 | 听 | 说 | 读 | 写 |
| 甲 | 85 | 78 | 85 | 73 |
| 乙 | 73 | 80 | 82 | 83 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2+bx+c经过A(-1,0),C(0,3)两点,点B是抛物线与x轴另一个交点,抛物线的对称轴DE交抛物线于点D,交x轴于点E,点P在直线DE上,过C作CF⊥DE,垂足为点F,连接CP,过点P作PQ⊥CP,交x轴于点Q.设点P的纵坐标为m.
如图,抛物线y=-x2+bx+c经过A(-1,0),C(0,3)两点,点B是抛物线与x轴另一个交点,抛物线的对称轴DE交抛物线于点D,交x轴于点E,点P在直线DE上,过C作CF⊥DE,垂足为点F,连接CP,过点P作PQ⊥CP,交x轴于点Q.设点P的纵坐标为m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com