
分析 (1)根据题意即可得到结论;
(2)设安排甲零件的产量x万件,则安排乙零件的产量(80-x)万件,根据题意得到10x+8(80-x)≤740,解不等式即可得到结论;
(3)甲种零件售价提高m元时,可获总利润w元,根据题意得到合适解析式,根据二次函数的性质即可得到结论.
解答 解:(1)根据题意得:y=(16-10)x+(12-8)(80-x),
即y与x的函数关系式是y=2x+320;
(2)设安排甲零件的产量x万件,则安排乙零件的产量(80-x)万件,
根据题意得:10x+8(80-x)≤740,
解得:x≤50,
由(1)知y=2x+320,
∵2>0,y随x的增大而增大,
∴当x=50时,y有最大值,y最大=2×50+320=420,
此时80-50=30(万件).
答:安排甲零件的产量50万件,则安排乙零件的产量30万件,可使所获的总利润最大,最大总利润是420万元;
(3)甲种零件售价提高m元时,可获总利润w元,
则w=(16+m-10)(50-5m)+(12-8)[80-(50-5m)],
∴w=-5m2+40m+420=-5(m-4)2+500,
∵-5<0,开口向下,
∴w有最大值,
当m=4时,w最大=500.
答:甲零件售价提高4元时,可获总利润最大,最大总利润是500万元.
点评 本题考查的是用二次函数解决实际问题,此类题是近年中考中的热点问题.注意利用二次函数求最值时,关键是应用二次函数的性质;即由函数w随m的变化,结合自变量的取值范围确定最值.


科目:初中数学 来源: 题型:选择题
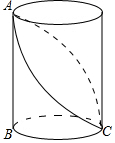 如图,已知圆柱的底面直径BC=$\frac{6}{π}$,高AB=3,小虫在圆柱表面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为( )
如图,已知圆柱的底面直径BC=$\frac{6}{π}$,高AB=3,小虫在圆柱表面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为( )| A. | $3\sqrt{2}$ | B. | $3\sqrt{5}$ | C. | $6\sqrt{5}$ | D. | $6\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两人要测量灯塔AB的高度,甲在C处用高度为1.5米的侧角仪测得塔顶A的仰角为72°,乙在E处用高度为1.8米的测角仪测得塔顶A的仰角为50°,点B、C、E在同一条直线上,且甲乙两人的距离CE=10米,请你根据所测量的数据计算灯塔AB的高度.(结果精确到0.1m)(参考数据:sin50°≈$\frac{4}{5}$,cos50°≈$\frac{16}{25}$,tan50°≈$\frac{5}{4}$,sin72°≈$\frac{19}{20}$,cos72°≈$\frac{3}{10}$,tan72°≈$\frac{19}{6}$)
甲、乙两人要测量灯塔AB的高度,甲在C处用高度为1.5米的侧角仪测得塔顶A的仰角为72°,乙在E处用高度为1.8米的测角仪测得塔顶A的仰角为50°,点B、C、E在同一条直线上,且甲乙两人的距离CE=10米,请你根据所测量的数据计算灯塔AB的高度.(结果精确到0.1m)(参考数据:sin50°≈$\frac{4}{5}$,cos50°≈$\frac{16}{25}$,tan50°≈$\frac{5}{4}$,sin72°≈$\frac{19}{20}$,cos72°≈$\frac{3}{10}$,tan72°≈$\frac{19}{6}$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
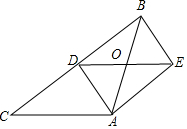 如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.
如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com