

 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
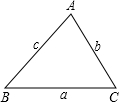 如图,在锐角△ABC中,a>b>c,以某任意两个顶点为顶点作矩形,第三个顶点落在以这两个顶点所确定的对边上,这样可以作三个面积相等的矩形,请问这三个矩形的周长大小关系如何?(记ta、tb、tc分别以a、b、c为边的矩形的周长)答:
如图,在锐角△ABC中,a>b>c,以某任意两个顶点为顶点作矩形,第三个顶点落在以这两个顶点所确定的对边上,这样可以作三个面积相等的矩形,请问这三个矩形的周长大小关系如何?(记ta、tb、tc分别以a、b、c为边的矩形的周长)答:查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 24、阅读材料,解决问题.
24、阅读材料,解决问题.
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源:2010-2011学年北京市考数学一模试卷 题型:解答题
认真阅读下列问题,并加以解决:
问题1:如图1,△ABC是直角三角形,∠C =90º.现将△ABC补成一个矩形.要求:使△ABC的两个顶点成为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上.请将符合条件的所有矩形在图1中画出来;


图1 图2
问题2:如图2,△ABC是锐角三角形,且满足BC>AC>AB,按问题1中的要求把它补成矩形.请问符合要求的矩形最多可以画出 个,并猜想它们面积之间的数量关系是 (填写“相等”或“不相等”);
问题3:如果△ABC是钝角三角形,且三边仍然满足BC>AC>AB,现将它补成矩形.要求:△ABC有两个顶点成为矩形的两个顶点,第三个顶点落在矩形的一边上,那么这几个矩形面积之间的数量关系是 (填写“相等”或“不相等”).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com