
【题目】在平面直角坐标系中,直线y=![]() x+b与x轴交于点A,与y轴交于点B,点P坐标为(3,0),过点P作PC⊥x轴于P,且△ABC为等腰直角三角形.
x+b与x轴交于点A,与y轴交于点B,点P坐标为(3,0),过点P作PC⊥x轴于P,且△ABC为等腰直角三角形.
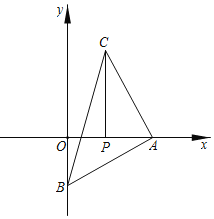
(1)如图,当∠BAC=90°,AB=AC时,求证△ABO≌△CAP;
(2)当AB为直角边时,请直接写出所有可能的b值.
【答案】(1)证明见解析;(2)当AB为直角边时,所有可能的b值为﹣3或3或﹣1.
【解析】
(1)通过题意可得∠CPA=∠AOB=90°,AB=CA,再根据互余的性质求出∠OAB=∠PCA,即可证明.
(2)将直线在坐标轴上平移即可分三类情况讨论.
(1)证明:∵∠BAC=90°,
∴∠OAB+∠CAP=90°,
∵PC⊥x轴,
∴∠CPA=90°,
∴∠PCA+∠CAP=90°,
∴∠OAB=∠PCA,
∵∠AOB=90°,
∴∠AOB=∠CPA,
在△ABO和△CAP中,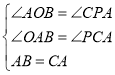 ,
,
∴△ABO≌△CAP(AAS);
(2)解:分三种情况:
①如图1所示:

∵直线y=![]() x+b与x轴交于点A,与y轴交于点B,
x+b与x轴交于点A,与y轴交于点B,
∴A(﹣2b,0),B(0,b),
∴OA=﹣2b,OB=﹣b,
∵点P坐标为(3,0),
∴OP=3,
由(1)得:△ABO≌△CAP(AAS),
∴OB=AP=﹣b,
∴OP=OA﹣AP=﹣b=3,
∴b=﹣3;
②如图2所示:
作CM⊥y轴于M,则CM=OP=3,
同①得:△ABO≌△BCM(AAS),
∴OB=CM=3,
∴b=3;
③如图3所示:
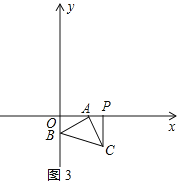
同①得:△ABO≌△CAP(AAS),
∴OB=AP=﹣b,
∵OA=﹣2b,OA+AP=3,
∴﹣2b﹣b=3,
∴b=﹣1;
综上所述,当AB为直角边时,所有可能的b值为﹣3或3或﹣1.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 轴上一个动点,
轴上一个动点,![]()
(1)如图1,当![]() ,且
,且![]() 按逆时针方向排列,求
按逆时针方向排列,求![]() 点的坐标.
点的坐标.
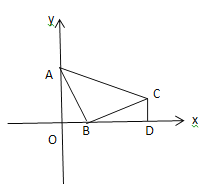
(图1)
(2)如图2,当![]() ,且
,且![]() 按顺时针方向排列,
按顺时针方向排列,![]() 连
连![]() 交
交![]() 轴于
轴于![]() ,求证:
,求证:![]()
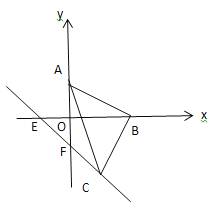
(图2)
(3)如图3,m>2,且![]() 按顺时针方向排列,若
按顺时针方向排列,若![]() 两点关于直线
两点关于直线![]() 的的对称点,画出图形并用含
的的对称点,画出图形并用含![]() 的式子表示
的式子表示![]() 的面积
的面积![]()
图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 是一次函数
是一次函数![]() 的图象,直线
的图象,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且经过点
,且经过点![]() ,直线
,直线![]() 交于点
交于点![]() ,
,
(1)求点![]() ,点
,点![]() 的坐标;
的坐标;
(1)求直线![]() 的表达式;
的表达式;
(3)求![]() 的面积.
的面积.
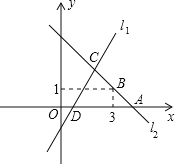
查看答案和解析>>
科目:初中数学 来源: 题型:
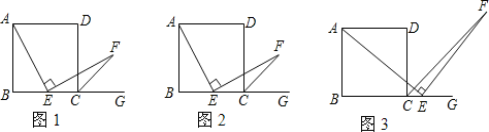
【题目】数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线CF于点F,求证:AE=EF.
经过思考,小明展示了一种正确的解题思路:在AB上截取BM=BE,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立。你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解居民的环保意识,社区工作人员在某小区随机抽取了若干名居民开展有奖问卷调查活动,并用得到的数据绘制了如下条形统计图.请根据图中信息,解答下列问题.

(1)求本次调查获取的样本数据的平均数;
(2)如果对该小区的800名居民全面开展这项有奖问卷活动,得10分者设为一等奖,请你根据调查结果,估计需准备多少份一等奖奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
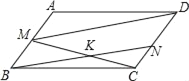
【题目】在ABCD中,AB=1,BC=2,∠B=45°,M为AB的中点.
(1)求tan∠CMD的值;
(2)设N为CD中点,CM交BN于K,求![]() 及S△BKC的值.
及S△BKC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国的农作物主要以水稻、玉米和小麦为主,种植太单调不利于土壤环境的维护,而且对农业的发展也没有促进作用,为了鼓励大豆的种植,国家对种植大豆的农民给予补贴,调动农民种植大豆的积极性.我市乃大豆之乡,今年很多合作社调整种植结构,把种植玉米改成种植大豆,今年我市某合作社共收获大豆200吨,计划采用批发和零售两种方式销售.经市场调查,批发平均每天售出14吨,由于今年我市小型大豆深加工企业的增多,预计能提前完成销售任务,在平均每天批发量不变的情况下,实际平均每天的零售量比原计划的2倍还多14吨,结果提前5天完成销售任务。那么原计划零售平均每天售出多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=CB,F为AB延长线上一点,点E在BC上,且AE=CF,若∠CAE=32°,则∠ACF的度数为__________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.

(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com