
【题目】已知四边形ABCD是平行四边形,AD=BD,过点D作DE⊥AB于点E,过点A作AH⊥BD于点H,交DE、BC分别于点F、G,连接CF.

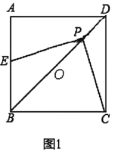
(1)如图1,求证:∠BAG=∠FCB;
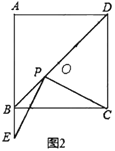
(2)如图2,过点A作AK平分∠DAF交ED于点K,若AK=1,∠FCD=45°,求DF的长;
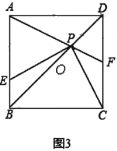
(3)如图3,若AD=10,DH=6,求CF的长.
【答案】(1)见解析;(2)DF=![]() ;(3)CF=
;(3)CF=![]() .
.
【解析】
(1)本题连接BF.设∠BAG=x,∠DAG=y,由∠BDE+∠DFH=90°,∠BAG+∠AFE=90°,∠DFH=∠AFE(对顶角相等)得∠BDE=∠BAG.再通过角之间的关系,证明∠FDC+∠FBC=180°从而得到点F、B、C、D四点共圆,所以∠FCB=∠BDE=x,可证明∠BAG=∠FCB.
(2)本题主要根据平行四边形的性质得出∠BAD=∠BCD,又由(1)∠BAG=∠FCB,得∠DAF=∠FCD=45°,因为AH⊥BD进而得到∠ADH=45°,这样又因为∠FAK=∠DAK=22.5°,∠ADE=∠BDE=22.5°,这样就可以利用角之间的关系找到线段之间的关系,求出DF的长.
(3)连接BF,本题主要利用勾股定理求出AH、FH的长,再在Rt△AHB和Rt△FHD中,分别表示出AB2和DF2,这样就可以在Rt△FDC中,利用勾股定理,求出CF的长度.
(1)如图1,连接BF.
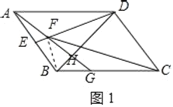
设∠BAG=x,∠DAG=y
∵AD=BD,DE⊥AB于点E
∴直线DE是等腰三角形的对称轴
∴∠ABF=∠BAG=x,∠DBF=∠DAG=y,∠ADE=∠BDE
∴∠ABD=∠BAD=∠BAG+∠DAG=x+y
∵AH⊥BD于点H
∴∠AHD=90°∴∠BDE+∠DFH=90°
∵∠BAG+∠AFE=90°,∠DFH=∠AFE(对顶角相等)
∴∠BDE=∠BAG=x
∴∠ADE=∠BDE=x,∠ADB=∠ADE+∠BDE=2x
∵ABCD
∴AD∥BC,AB∥CD
∴∠DBC=∠ADB=2x,∠CDB=∠ABD=x+y
∴∠FDC=∠BDE+∠CDB=x+x+y=2x+y,∠FBC=∠DBF+∠DBC=y+2x
∴∠FDC+∠FBC=4x+2y
∵AB∥CD
∴∠BAD+∠ADC=180°
∵∠BAD=∠BAG+∠DAG=x+y,∠ADC=∠ADB+∠CDB=2x+x+y=3x+y
∴x+y+3x+y=180°
∴4x+2y=180°
∴∠FDC+∠FBC=4x+2y=180°
∴点F、B、C、D四点共圆
∴∠FCB=∠BDE=x
∴∠BAG=∠FCB
(2)如图2,连接BF,作FM⊥AK于点M.
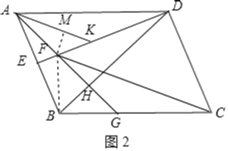
∵四边形ABCD是平行四边形
∴∠BAD=∠BCD
由(1)知,∠BAG=∠FCB
∴∠DAF=∠FCD=45°
∵AH⊥BD
∴∠ADH=45°
由(1)知,∠ADE=∠BDE
∴∠ADE=∠BDE=22.5°
∵AK
∴∠DAK=∠FAK=![]() ∠DAF=22.5°
∠DAF=22.5°
∴∠DAK=∠ADE
∴DK=AK=1
∵∠AKE=∠DAK+∠ADE=45°,DE⊥AB
∴AE=EK=![]() AK=
AK=![]() ,∠EAK=45°
,∠EAK=45°
∴∠BAG=∠EAK﹣∠FAK=22.5°
∴∠BAG=∠FAK
∵FM⊥AK,FE⊥AB
∴FE=FM
在Rt△FMK中,∠FMK=90°,∠AKE=45°
∴FK=![]() FM=
FM=![]() FE
FE
∵FE+FK=EK
∴FE+![]() FE=
FE=![]()
∴FE=![]()
∴FK=![]() ﹣1
﹣1
∴DF=FK+DK=![]()
(3)如图3,连接BF.
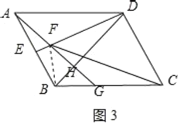
∵AH⊥BD,AD=10,DH=6
∴根据勾股定理得,AH=8
∵BD=AD=10
∴BH=BD﹣DH=4
由(1)知,BF=AF,设FH=a,则BF=AF=8﹣a
由勾股定理得42+a2=(8﹣a)2
∴a=3
∴在Rt△FHD中,∠FHD=90°
由勾股定理得DF2=FH2+DH2=32+62=45
在Rt△AHB中,∠AHB=90°
由勾股定理得AB2=AH2+BH2=82+42=80
∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD
∴∠FDC=∠AED
∵DE⊥AB
∴∠AED=90°
∴∠FDC=90°
∴在R△FDC中,根据勾股定理得CF2=CD2+DF2=AB2+DF2=80+45=125,
∴CF=![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
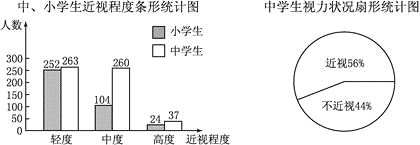
【题目】某市青少年健康研究中心随机抽取了本市1000名小学生和若干名中学生,对他们的视力状况进行了调查,并把调查结果绘制成如下统计图.(近视程度分为轻度、中度、高度三种)
(1)求这1000名小学生患近视的百分比.
(2)求本次抽查的中学生人数.
(3)该市有中学生8万人,小学生10万人.分别估计该市的中学生与小学生患“中度近视”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 上任意一点(不与
上任意一点(不与![]() 、
、![]() 重合),点
重合),点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() .
.
初步感知:当点![]() 与点
与点![]() 重合时,比较:
重合时,比较:![]()
![]() (选填“
(选填“![]() ”、“
”、“![]() ”或“
”或“![]() ”).
”).
再次感知:如图1,当点![]() 在线段
在线段![]() 上时,如何判断
上时,如何判断![]() 和
和![]() 数量关系呢?
数量关系呢?
甲同学通过过点![]() 分别向
分别向![]() 和
和![]() 作垂线,构造全等三角形,证明出
作垂线,构造全等三角形,证明出![]() ;
;
乙同学通过连接![]() ,证明出
,证明出![]() ,
,![]() ,从而证明出
,从而证明出![]() .
.
理想感悟:如图2,当点![]() 落在线段
落在线段![]() 上时,判断
上时,判断![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
拓展应用:连接![]() ,并延长
,并延长![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)当![]() 时,如图3,直接写出
时,如图3,直接写出![]() 的面积为 ;
的面积为 ;
(2)直接写出![]() 面积
面积![]() 的取值范围 .
的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(5,0),与y轴交于点C(0,![]() ),顶点为D,对称轴交x轴于点E.
),顶点为D,对称轴交x轴于点E.
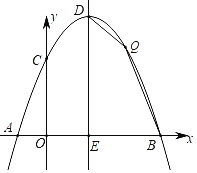
(1)求该抛物线的一般式;
(2)若点Q为该抛物线上第一象限内一动点,且点Q在对称轴DE的右侧,求四边形DEBQ面积的最大值及此时点Q的坐标;
(3)若点P为对称轴DE上异于D,E的动点,过点D作直线PB的垂线交直线PB于点F,交x轴于点G,当△PDG为等腰三角形时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校学生每周参加课外辅导班的情况,随机调査了部分学生一周内参加课外辅导班的学科数,并将调查结果绘制成如图1、图2所示的两幅不完整统计图(其中A:0个学科,B:1个学科,C:2个学科,D:3个学科,E:4个学科或以上),请根据统计图中的信息,解答下列问题:
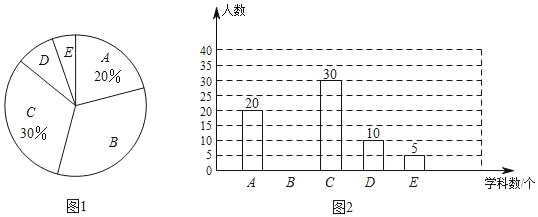
(1)请将图2的统计图补充完整;
(2)根据本次调查的数据,每周参加课外辅导班的学科数的众数是 个学科;
(3)若该校共有2000名学生,根据以上调查结果估计该校全体学生一周内参加课外辅导班在3个学科(含3个学科)以上的学生共有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:

(1)此次共调查了多少人?
(2)求文学社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有1500名学生,请估计喜欢体育类社团的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、图②,在给定的一张矩形纸片上作一个正方形,甲、乙两人的作法如下:
甲:以点A为圆心,AD长为半径画弧,交AB于点E,以点D为圆心,AD长为半径画弧,交CD于点F,连接EF,则四边形AEFD即为所求;
乙:作∠DAB的平分线,交CD于点M,同理作∠ADC的平分线,交AB于点N,连接MN,则四边形ADMN即为所求.


对于以上两种作法,可以做出的判定是( )
A.甲正确,乙错误B.甲、乙均正确
C.乙正确,甲错误D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】篮球运动是全世界最流行的运动之一,近年流行于青少年之间的“3对3”篮球将登上2020年奥运会赛场,为备战某市中学生“3对3”篮球联赛,某校甲、乙、丙三位同学作为“兄弟战队”的主力队员进行篮球传球训练,篮球由一个人随机传给另一个人,且每位传球人传球给其余两人的机会是均等的,现在由甲开始传球.
(1)求甲第一次传球给乙的概率;
(2)三次传球后,篮球在谁手中的可能性大?请利用树状图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为______.
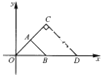
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com