
分析 (1)根据两个月分别用水12m3时交水费44.8元和用水14m3时交水费53.2元,建立方程组求解即可;
(2)设用水低谷期的用水量为y立方米,则用水高峰期的用水量为(1-20%)y立方米,利用水费44.8作为相等关系建立方程可求得水低谷期的用水量和高峰期的用水量,再求得总的用水量,用作差法即可比较即可.
解答 解:(1)由题意得,$\left\{\begin{array}{l}{8a+(12-8)b=44.8}\\{8a+(14-8)b=53.2}\end{array}\right.$,
解方程组得,$\left\{\begin{array}{l}{a=3.5}\\{b=4.2}\end{array}\right.$,
即:a,b的值为3.5元和4.2元;
(2)设用水低谷期的用水量为y立方米,则用水高峰期的用水量为(1-20%)y立方米,
由题意得:3.2y+4×(1-20%)y=44.8,
解得:y=7,
∴y+(1-20%)y=7+5.6=12.6,
∵12.6-12=0.6(立方米).
∴问题(1)中的方案下的用水量较少,少0.6立方米.
点评 此题是二元一次方程组的应用,还涉及到一元一次解方程和二元一次方程组,解本题的关键是用每月所交水费建立方程或方程组,解此类题目要审清题意,找出相等关系.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:解答题
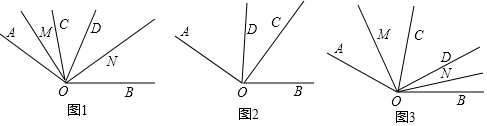
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
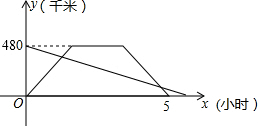 一辆动车和一辆普快分别从A、B两地同时出发相向而行,动车到达B地停留1小时后原速返回A地,结果比普快早1小时到达A地,它们离A地的路程随时间变化的图象如图所示,则下列结论中正确的个数是( )
一辆动车和一辆普快分别从A、B两地同时出发相向而行,动车到达B地停留1小时后原速返回A地,结果比普快早1小时到达A地,它们离A地的路程随时间变化的图象如图所示,则下列结论中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
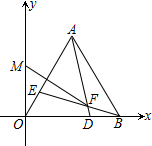 如图,在平面直角坐标系中,等边△OAB的边OB在x轴正半轴上,点A(3,m),m>0,点D、E分别从B、O以相同的速度向O、A运动,连接AD、BE,交点为F,M是y轴上一点,则FM的最小值是( )
如图,在平面直角坐标系中,等边△OAB的边OB在x轴正半轴上,点A(3,m),m>0,点D、E分别从B、O以相同的速度向O、A运动,连接AD、BE,交点为F,M是y轴上一点,则FM的最小值是( )| A. | 3 | B. | $\sqrt{3}$+1 | C. | 2$\sqrt{3}$-2 | D. | 6-2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
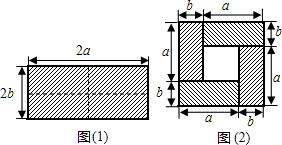
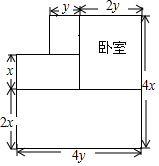 如图,是张老师买的经济适用房平面结构示意图,图中标明了有关尺寸(墙体厚度忽略不计,单位:m),房主计划把卧室以外的地面都铺上地砖,
如图,是张老师买的经济适用房平面结构示意图,图中标明了有关尺寸(墙体厚度忽略不计,单位:m),房主计划把卧室以外的地面都铺上地砖,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com