已知:二次函数y=x2-kx+k+4的图象与y轴交于点C,且与x轴的正半轴交于A、B两点(点A在点B左侧).若A、B两点的横坐标为整数,
(1)确定这个二次函数的解析式并求它的顶点坐标;
(2)若点D的坐标是(0,6),点P(t,0)是线段AB上的一个动点,它可与点A重合,但不与点B重合.设四边形PBCD的面积为S,求S与t的函数关系式;
(3)若点P与点A重合,得到四边形ABCD,以四边形ABCD的一边为边,画一个三角形,使它的面积等于四边形ABCD的面积,并注明三角形高线的长.再利用“等底等高的三角形面积相等”的知识,画一个三角形,使它的面积等于四边形ABCD的面积(画示意图,不写计算和证明过程).
分析:(1)令y=0,不难得出方程的△>0;关键是方程的整数根,整除和奇偶性问题.根据(k-2+m)(k-2-m)=20得出k-2+m是k-2-m是同奇、同偶的两数是解题的关键.
(由于k-2+m+k-2-m=2k-4,因此两数的和为偶数,而偶数+偶数=偶数,奇数+奇数=偶数,奇数+偶数=奇数,因此两数必须为同奇同偶)
(本题也可用韦达定理来求)
(2)由于四边形PBCD不一定是规则的四边形,因此可用三角形OBC的面积-三角形ODP的面积来求.
(3)本题答案不唯一,只要正确都行.
解答:解:(1)依题意可设A(a,0),B(b,0);
令y=0,则a、b是x
2-kx+k+4=0的两根.
于是△=(-k)
2-4(k+4)=k
2-4k-16=(k-2)
2-20>0,且a+b=k;
∵a、b是不等的正整数,
∴k为正整数,且(k-2)
2-20是一个整数的平方.
设(k-2)
2-m
2=20,
即(k-2+m)(k-2-m)=20,
注意到k-2+m是k-2-m是同奇、同偶的两数,且20是偶数.
∴
;
,
;
,
解得:
;
;
;
,
∴k=8,
∴这个二次函数的解析式为y=x
2-8x+12,其顶点坐标为(4,-4).
(2)∵y=x
2-8x+12,
∴此二次函数的图形与y轴的交点C的坐标为(0,12),与y轴的交点A(2,0),B(6,0).
又S
四边形PBCD=S
△COB-S
△DOP,
∴S=
×12×6-
×6t,
∴S=36-3t(2≤t<6);
(3)∵AB=4,又S=30,
∴可设所画三角形为△MAB,AB边上的高为h.
∴S
△MAB=
×4×h,
∴h=15.
点评:本题结合四边形的性质考查二次函数的综合应用,有关函数和几何图形的综合题目,要利用几何图形的性质和二次函数的性质把数与形有机的结合在一起,利用题中所给出的面积和周长之间的数量关系求解.



 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.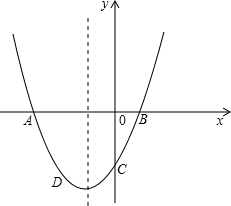 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.