
【题目】如图,在边长为4的菱形ABCD中,BD=4,E、F分别是AD、CD上的动点(包含端点),且AE+CF=4,连接BE、EF、FB.
(1)试探究BE与BF的数量关系,并证明你的结论;
(2)求EF的最大值与最小值.

【答案】(1)见解析(2)EF的最大值为4,最小值为![]() .
.
【解析】试题分析:(1)AE+CF=4,DF+CF=4,则DF=AE,根据题目已知条件可通过角边角证明![]() ,从而证明BE=BF(2)可先证明BEF为等边三角形。那么BE=BF=EF,点E在AD上运动,当BE
,从而证明BE=BF(2)可先证明BEF为等边三角形。那么BE=BF=EF,点E在AD上运动,当BE![]() AD时,BE最短,当E与A或D重合时最长。
AD时,BE最短,当E与A或D重合时最长。
解:(1)BE=BF,证明如下:
∵四边形ABCD是边长为4的菱形,BD=4,
∴△ABD、△CBD都是边长为4的正三角形,
∵AE+CF=4,
∴CF=4﹣AE=AD﹣AE=DE,
又∵BD=BC=4,∠BDE=∠C=60°,
在△BDE和△BCF中,
DE=DF,∠BDE=∠C,BD=BC,
∴△BDE≌△BCF(SAS),
∴BE=BF;
(2)∵△BDE≌△BCF,
∴∠EBD=∠FBC,
∴∠EBD+∠DBF=∠FBC+∠DBF,
∴∠EBF=∠DBC=60°,
又∵BE=BF,
∴△BEF是正三角形,
∴EF=BE=BF,
当动点E运动到点D或点A时,BE的最大值为4,
当BE⊥AD,即E为AD的中点时,BE的最小值为![]() ,
,
∵EF=BE,
∴EF的最大值为4,最小值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,已知直线![]() 和双曲线
和双曲线![]() (k>0),点A(m,n)在双曲线
(k>0),点A(m,n)在双曲线 ![]() 上.当m=n=2时.
上.当m=n=2时.
(1)直接写出k的值;
(2)将直线![]() 作怎样的平移能使平移后的直线与双曲线
作怎样的平移能使平移后的直线与双曲线 ![]() 只有一个交点.
只有一个交点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点BD是对角线,AG∥DB,交CB的延长线于G,连接GF,若AD⊥BD.下列结论:①DE∥BF;②四边形BEDF是菱形;③FG⊥AB;④S△BFG=![]() .其中正确的是( )
.其中正确的是( )

A. ①②③④ B. ①② C. ①③ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在节日期间开展优惠促销活动:凡购买原价超过200元的商品,超过200元的部分可以享受打折优惠若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)之间的函数关系的a图象如图所示,则图中a的值是( )
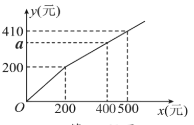
A.300B.320C.340D.360
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,点F在AC延长线上,![]() ,DE是△ABC中位线,如果∠1=30°,DE=2,则四边形AFED的周长是________
,DE是△ABC中位线,如果∠1=30°,DE=2,则四边形AFED的周长是________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.正确结论有( )

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
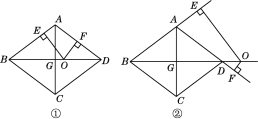
【题目】如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)求对角线AC的长及菱形ABCD的面积.
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com