
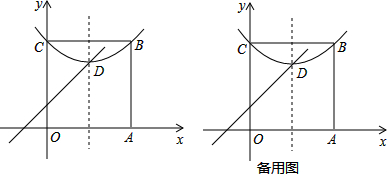
分析 (1)根据特征线直接求出点D的特征线;
(2)由点D的一条特征线和正方形的性质求出点D的坐标,从而求出抛物线解析式;
(2)分平行于x轴和y轴两种情况,由折叠的性质计算即可.
解答 解:(1)∵点D(m,n),
∴点D(m,n)的特征线是x=m,y=n,y=x+n-m,y=-x+m+n;
(2)点D有一条特征线是y=x+1,
∴n-m=1,
∴n=m+1
∵抛物线解析式为$y=\frac{1}{4}{({x-m})^2}+n$,
∴y=$\frac{1}{4}$(x-m)2+m+1,
∵四边形OABC是正方形,且D点为正方形的对称轴,D(m,n),
∴B(2m,2m),
∴$\frac{1}{4}$(2m-m)2+n=2m,将n=m+1带入得到m=2,n=3;
∴D(2,3),
∴抛物线解析式为y=$\frac{1}{4}$(x-2)2+3
(3)如图,当点A′在平行于y轴的D点的特征线时,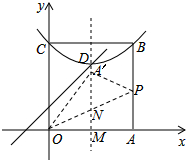
根据题意可得,D(2,3),
∴OA′=OA=4,OM=2,
∴∠A′OM=60°,
∴∠A′OP=∠AOP=30°,
∴MN=$\frac{OM}{\sqrt{3}}$=$\frac{2\sqrt{3}}{3}$,
∴抛物线需要向下平移的距离=3-$\frac{2\sqrt{3}}{3}$=$\frac{9-2\sqrt{3}}{3}$.
如图,当点A′在平行于x轴的D点的特征线时,设A′(p,3),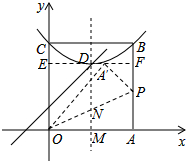
则OA′=OA=4,OE=3,EA′=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
∴A′F=4-$\sqrt{7}$,
设P(4,c)(c>0),
,在Rt△A′FP中,(4-$\sqrt{7}$)2+(3-c)2=c2,
∴c=$\frac{16-4\sqrt{7}}{3}$,
∴P(4,$\frac{16-4\sqrt{7}}{3}$)
∴直线OP解析式为y=$\frac{4-\sqrt{7}}{3}$x,
∴N(2,$\frac{8-2\sqrt{7}}{3}$),
∴抛物线需要向下平移的距离=3-$\frac{8-2\sqrt{7}}{3}$=$\frac{1+2\sqrt{7}}{3}$,
即:抛物线向下平移$\frac{9-2\sqrt{3}}{3}$或$\frac{1+2\sqrt{7}}{3}$距离,其顶点落在OP上.
点评 此题是二次函数综合题,主要考查了折叠的性质,正方形的性质,特征线的理解,解本题的关键是用正方形的性质求出点D的坐标.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 同位角相等 | |
| B. | 三角形的三个内角中,至少有一个不大于60° | |
| C. | 任何数的零次幂都是1 | |
| D. | 垂直于同一直线的两条直线互相垂直 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
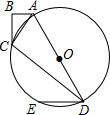 如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E
如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x | B. | y=2x | C. | y=kx+2k+1(k≠1) | D. | y=kx-2k+1(k≠0) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
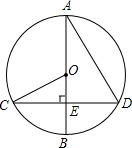 如图,CD为⊙O的弦,直径AB为4,AB⊥CD于E,∠A=30°,则$\widehat{BC}$的长为$\frac{2}{3}$π(结果保留π).
如图,CD为⊙O的弦,直径AB为4,AB⊥CD于E,∠A=30°,则$\widehat{BC}$的长为$\frac{2}{3}$π(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com