
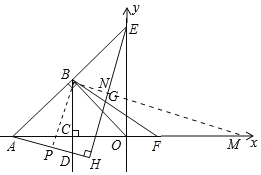
【题目】如图,在平面直角坐标系中,O为坐标原点,等腰直角三角形OAB的斜边AO在x轴上![]() ,
,![]() ,点B的坐标为
,点B的坐标为![]() .
.

(1)求A点坐标;
(2)过B作![]() 轴于C,点D从B出发沿射线BC以每秒2个单位的速度运动,连接AD、OD,动点D的运动时间为t,
轴于C,点D从B出发沿射线BC以每秒2个单位的速度运动,连接AD、OD,动点D的运动时间为t,![]() 的面积为S,求S与t的数量关系,并直接写出t的取值范围;
的面积为S,求S与t的数量关系,并直接写出t的取值范围;
(3)在(2)的条件下,当点D运动到x轴下方时,延长AB交y轴于E,过E作![]() 于H,在x轴正半轴上取点F,连接BF交EH于G,
于H,在x轴正半轴上取点F,连接BF交EH于G,![]() ,当
,当![]() 时,求点D的坐标.
时,求点D的坐标.
【答案】(1)A(﹣14,0);(2)S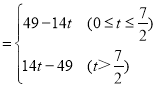 ;(3)D(﹣7,
;(3)D(﹣7,![]() )或(﹣7,﹣21).
)或(﹣7,﹣21).
【解析】
(1)作BH⊥OA于H.理由等腰直角三角形的性质求出OA即可解决问题;
(2)如图2中,分两种情形当0≤t![]() 时,当t
时,当t![]() 时,分别求解即可解决问题;
时,分别求解即可解决问题;
(3)如图3中,作BM∥AH交EH于N,BP⊥AD于P.理由相似三角形的性质证明EH=2AH,解直角三角形求出EH,AH,设H(m,n),构建方程组求出m,n,求出直线AH的解析式即可解决问题.
(1)作BH⊥OA于H.
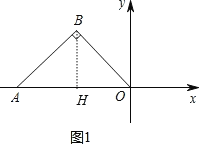
∵BA=BO,∠ABO=90°,∴BH=AH=OH.
∵B(﹣7,7),∴AH=BH=OH=7,∴OA=14,∴A(﹣14,0).
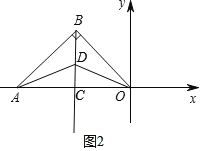
(2)如图2中,当0≤t![]() 时,S
时,S![]() 14×(7﹣2t)=49﹣14t
14×(7﹣2t)=49﹣14t
当t![]() 时,S
时,S![]() 14×(2t﹣7)=14t﹣49.
14×(2t﹣7)=14t﹣49.
综上所述:S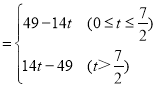 .
.
(3)如图3中,作BM∥AH交EH于N,BP⊥AD于P.
∵BP⊥AH,EH⊥AH,∴BP∥EH.
∵AB=BE,∴AP=PH,∴PB![]() EH.
EH.
∵BN∥AH,∴EN=NH,
∴BN![]() AH,∠BNG=∠BPD=90°.
AH,∠BNG=∠BPD=90°.
∵BM∥AH,∴∠BMF=∠MAH.
∵∠AFB=2∠OAD=∠FMB+∠FBM,
∴∠FBM=∠FMB=∠OAD.
∵∠OAD+∠ADC=90°,∠PBD+∠ADC=90°,
∴∠OAD=∠PBD,∴∠PBD=∠NBG.
∵∠BPD=∠BNG=90°,∴△BPD∽△BNG,
∴![]() 2,∴BP=2BN,∴EH=2AH.
2,∴BP=2BN,∴EH=2AH.
在Rt△AEH中,∵AE=14![]() ,EH=2AH,
,EH=2AH,
∴EH![]() ,AH
,AH![]() ,
,
设H(m,n),则有: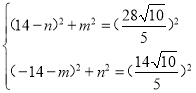 ,
,
解得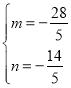 或
或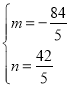 ,
,
∴H(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
易求直线AH的解析式为y![]() x
x![]() 或y=﹣3x﹣42,令x=-7,得:y=
或y=﹣3x﹣42,令x=-7,得:y=![]() 或﹣21,
或﹣21,
∴D(﹣7,![]() )或(﹣7,﹣21).
)或(﹣7,﹣21).


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】下列说法:①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1:2;④两个相似多边形的面积比为4:9,则周长的比为16:81中,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是

A.①②③ B.①②④ C.②③④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一次函数图象如图,
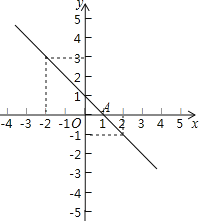
(1)求一次函数的解析式;
(2)若点P为该一次函数图象上一动点,且点A为该函数图象与x轴的交点,若S△OAP=2,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索题:(x﹣1)(x+1)=x2﹣1;
(x﹣1)(x2+x+1)=x3﹣1;
(x﹣1)(x3+x2+x+1)=x4﹣1;
(x﹣1)(x4+x3+x2+x+1)=x5﹣1
…
根据前面的规律,回答下列问题:
(1)(x﹣1)(xn+xn﹣1+xn﹣2+…+x3+x2+x+1)=_____.
(2)当x=3时,(3﹣1)(32015+32014+32013+…+33+32+3+1)=______.
(3)求:22014+22013+22012+…+23+22+2+1的值.(请写出解题过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com