练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    设m=2002+2001×2002+2001×20022+…+2001×20022000，n=20022001．则正确的关系是（　　）
    A、m=n×2001B、m=nC、m=n÷2002D、m=n+2002
    分析：将第二项到最后一项中的2001提出，括号中即为关于2002的等比数列的和，运用等比数列求和公式即可计算m的值．
    解答：解：m=2002+2001×（2002+20022+20023+…+20022000）=2002+
    2002(1-20022000)
    1-2002
    ×2001=20022001=n
    故答案选B．
    点评：本题主要运用等比数列求和公式进行计算，计算量较大，但思路较简单．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    18、襄樊市认真落实国家关于减轻农民负担，增加农民收入的政策，从2003年开始减征农业税，2002年至2004年征收农业税变化情况见表（1），2004年市政府为了鼓励农民多种粮食，实行保护价收购，并对种植优质水稻（如中籼稻）另给予每亩15元的补贴（摘自《襄樊日报》2004年5月5日消息）．我市农民李江家有4个劳动力，承包20亩土地，今年春季全部种植中籼稻和棉花，种植中籼稻和棉花每亩所需劳力和预计每亩平均产值见表（2）设2004年李江家种植中籼稻和棉花的预计总收入为P元，种植中籼稻的土地为x亩．
    （1）李江家从国家开始减征农业税后两年可少交农业税多少元？
    （2）若不考虑上缴农业税，请写出P（元）与x（亩）的函数关系式；
    （3）李江家在不考虑他人帮工等其它因素的前提下，怎样安排中籼稻和棉花的种植面积才能保证P最大最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源：2010年湖北省黄冈市初一上学期期末模拟数学卷 题型：解答题

    现将连续自然数1至2009按图中的方式排列成一个长方形队列，再用正方形任意框出16个数。

     
    		 
    		 
    		 
     
    		 
    		 
    		 
     
    		 
    		 
    		 
     
    		 
    		 
    		 
     

    1      2      3      4     5      6      7
    8          9          10         11         12         13      14
    15         16         17         18         19         20      21
    22         23         24         25         26         27      28
    ·        ·        ·        ·        ·        ·     ·
    ·        ·        ·        ·        ·        ·     ·
    ·        ·        ·        ·        ·        ·     ·
    1996      1997     1998     1999     2000     2001  2002
    2003      2004     2005     2006     2007     2008  2009

     
     


    （1）设任意一个这样的正方形框中的最小数为，请用的代数式表示该框中的16个数，然后填入右表中相应的空格处，并求出这16个数中的最小数和最大数，然后填入右表中相应的空格处，并求出这16个数的和。（用的代数式表示）
    （2）在图中，要使一个正方形框出的16个数之和和分别等于832、2000、2008是否可能？若不可能，请说明理由；若可能，请求出该正方形框出的16个数中的最小数和最大数

    查看答案和解析>>

    科目：初中数学 来源：2002年全国中考数学试题汇编《二次函数》（03）（解析版） 题型：解答题

    （2002•桂林）某单位为响应政府发出的全民健身的号召，打算在长和宽分别为20m和11m的矩形大厅内修建一个60m2的矩形健身房ABCD．该健身房的四面墙壁中有两侧沿用大厅的旧墙壁（如图为平面示意图），已知装修旧墙壁的费用为20元/m2，新建（含装修）墙壁的费用为80元/m2．设健身房的高为3m，一面旧墙壁AB的长为xm，修建健身房墙壁的总投入为y元．
    （1）求y与x的函数关系式；
    （2）为了合理利用大厅，要求自变量x必须满足条件：8≤x≤12，当投入的资金为4800元时，问利用旧墙壁的总长度为多少？

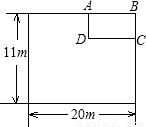
    查看答案和解析>>

    科目：初中数学 来源：2002年广西桂林市中考数学试卷（解析版） 题型：解答题

    （2002•桂林）某单位为响应政府发出的全民健身的号召，打算在长和宽分别为20m和11m的矩形大厅内修建一个60m2的矩形健身房ABCD．该健身房的四面墙壁中有两侧沿用大厅的旧墙壁（如图为平面示意图），已知装修旧墙壁的费用为20元/m2，新建（含装修）墙壁的费用为80元/m2．设健身房的高为3m，一面旧墙壁AB的长为xm，修建健身房墙壁的总投入为y元．
    （1）求y与x的函数关系式；
    （2）为了合理利用大厅，要求自变量x必须满足条件：8≤x≤12，当投入的资金为4800元时，问利用旧墙壁的总长度为多少？

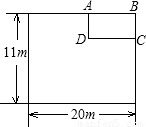
    查看答案和解析>>

    科目：初中数学 来源：2002年全国中考数学试题汇编《一元二次方程》（03）（解析版） 题型：填空题

    （2002•大连）大连市某乡无公害蔬菜的产量在两年内从20吨增加到35吨，设这两年无公害蔬菜的产量的年平均增长率为x，根据题意，列出方程为    ．

    查看答案和解析>>

    同步练习册答案