
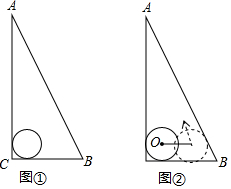
 如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.
如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.分析 (1)作∠ACB的平分线得出圆的一条弦,再作此弦的中垂线可得圆心O,作射线CO即可;
(2)添加如图所示辅助线,圆心O的运动路径长为${C}_{△O{O}_{1}{O}_{2}}$,先求出△ABC的三边长度,得出其周长,证四边形OEDO1、四边形O1O2HG、四边形OO2IF均为矩形、四边形OECF为正方形,得出∠OO1O2=60°=∠ABC、∠O1OO2=90°,从而知△OO1O2∽△CBA,利用相似三角形的性质即可得出答案.
解答 解:(1)如图①所示,射线OC即为所求;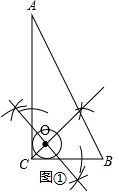
(2)如图,圆心O的运动路径长为${C}_{△O{O}_{1}{O}_{2}}$,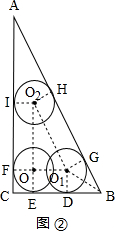
过点O1作O1D⊥BC、O1F⊥AC、O1G⊥AB,垂足分别为点D、F、G,
过点O作OE⊥BC,垂足为点E,连接O2B,
过点O2作O2H⊥AB,O2I⊥AC,垂足分别为点H、I,
在Rt△ABC中,∠ACB=90°、∠A=30°,
∴AC=$\frac{BC}{tan30°}$=$\frac{9}{\frac{\sqrt{3}}{3}}$=9$\sqrt{3}$,AB=2BC=18,∠ABC=60°,
∴C△ABC=9+9$\sqrt{3}$+18=27+9$\sqrt{3}$,
∵O1D⊥BC、O1G⊥AB,
∴D、G为切点,
∴BD=BG,
在Rt△O1BD和Rt△O1BG中,
∵$\left\{\begin{array}{l}{BD=BG}\\{{O}_{1}B={O}_{1}B}\end{array}\right.$,
∴△O1BD≌△O1BG(HL),
∴∠O1BG=∠O1BD=30°,
在Rt△O1BD中,∠O1DB=90°,∠O1BD=30°,
∴BD=$\frac{{O}_{1}D}{tan30°}$=$\frac{2}{\frac{\sqrt{3}}{3}}$=2$\sqrt{3}$,
∴OO1=9-2-2$\sqrt{3}$=7-2$\sqrt{3}$,
∵O1D=OE=2,O1D⊥BC,OE⊥BC,
∴O1D∥OE,且O1D=OE,
∴四边形OEDO1为平行四边形,
∵∠OED=90°,
∴四边形OEDO1为矩形,
同理四边形O1O2HG、四边形OO2IF、四边形OECF为矩形,
又OE=OF,
∴四边形OECF为正方形,
∵∠O1GH=∠CDO1=90°,∠ABC=60°,
∴∠GO1D=120°,
又∵∠FO1D=∠O2O1G=90°,
∴∠OO1O2=360°-90°-90°=60°=∠ABC,
同理,∠O1OO2=90°,
∴△OO1O2∽△CBA,
∴$\frac{{C}_{△O{O}_{1}{O}_{2}}}{{C}_{△ABC}}$=$\frac{{O}_{1}{O}_{2}}{BC}$,即$\frac{{C}_{△O{O}_{1}{O}_{2}}}{27+9\sqrt{3}}$=$\frac{7-2\sqrt{3}}{9}$,
∴${C}_{△O{O}_{1}{O}_{2}}$=15+$\sqrt{3}$,即圆心O运动的路径长为15+$\sqrt{3}$.
点评 本题主要考查作图-复杂作图、切线的判定与性质、矩形和正方形的判定与性质及相似三角形的判定与性质,熟练掌握切线的判定与性质、矩形和正方形的判定与性质及相似三角形的判定与性质是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
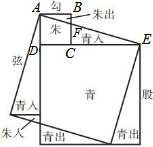 魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理,若图中BF=2,CF=4,则AE的长为6$\sqrt{10}$.
魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理,若图中BF=2,CF=4,则AE的长为6$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2a+3b=5ab | B. | $\sqrt{36}=±6$ | C. | a3b÷2ab=$\frac{1}{2}$a2 | D. | (2ab2)3=6a3b5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1+x2=-$\frac{5}{2}$ | B. | x1•x2=1 | C. | x1,x2都是有理数 | D. | x1,x2都是正数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 污水处理器型号 | A型 | B型 |
| 处理污水能力(吨/月) | 240 | 180 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com