
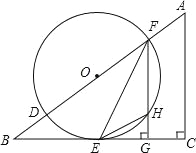
【题目】(2016广东省茂名市第24题)如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=![]() ∠A.
∠A.
(1)求证:BC是⊙O的切线;
(2)若sinB=![]() ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
【答案】(1)、证明过程见解析;(2)、![]()
【解析】
试题分析:(1)、首先连接OE,由在△ABC中,∠C=90°,FG⊥BC,可得FG∥AC,又由∠OFE=![]() ∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;(2)、由在△OBE中,sinB=
∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;(2)、由在△OBE中,sinB=![]() ,⊙O的半径为r,可求得OB,BE的长,然后由在△BFG中,求得BG,FG的长,则可求得EG的长,易证得△EGH∽△FGE,然后由相似三角形面积比等于相似比的平方,求得答案.
,⊙O的半径为r,可求得OB,BE的长,然后由在△BFG中,求得BG,FG的长,则可求得EG的长,易证得△EGH∽△FGE,然后由相似三角形面积比等于相似比的平方,求得答案.
试题解析:(1)、连接OE, ∵在△ABC中,∠C=90°,FG⊥BC, ∴∠BGF=∠C=90°, ∴FG∥AC,
∴∠OFG=∠A, ∴∠OFE=![]() ∠OFG, ∴∠OFE=∠EFG, ∵OE=OF, ∴∠OFE=∠OEF, ∴∠OEF=∠EFG,
∠OFG, ∴∠OFE=∠EFG, ∵OE=OF, ∴∠OFE=∠OEF, ∴∠OEF=∠EFG,
∴OE∥FG, ∴OE⊥BC, ∴BC是⊙O的切线;
(2)、∵在Rt△OBE中,sinB=![]() ,⊙O的半径为r, ∴OB=
,⊙O的半径为r, ∴OB=![]() r,BE=
r,BE=![]() r, ∴BF=OB+OF=
r, ∴BF=OB+OF=![]() r,
r,
∴FG=BFsinB=![]() r, ∴BG=
r, ∴BG=![]() =
=![]() r, ∴EG=BG﹣BE=
r, ∴EG=BG﹣BE=![]() r,
r,
∴S△FGE=![]() EGFG=
EGFG=![]() r2,EG:FG=1:2, ∵BC是切线, ∴∠GEH=∠EFG, ∵∠EGH=∠FGE,
r2,EG:FG=1:2, ∵BC是切线, ∴∠GEH=∠EFG, ∵∠EGH=∠FGE,
∴△EGH∽△FGE, ∴![]() =(
=(![]() )=
)=![]() , ∴S△EHG=
, ∴S△EHG=![]() S△FGE=
S△FGE=![]() r2.
r2.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
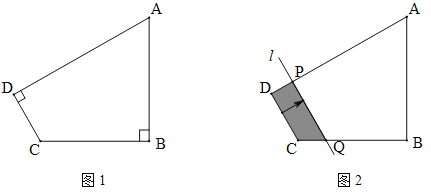
【题目】(2016四川省乐山市第23题)如图1,四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=![]() .
.
(1)求CD边的长;
(2)如图2,将直线CD边沿箭头方向平移,交DA于点P,交CB于点Q (点Q运动到点B停止),设DP=x,四边形PQCD的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出自变量
的函数关系式,并求出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列四种说法:①锐角的补角一定是钝角;②一个角的补角一定大于这个角;③如果两个角是同一个角的补角,那么它们相等;④锐角和钝角互补.其中正确的是( )
A.①②
B.①③
C.①②③
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
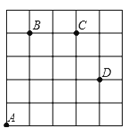
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负,如果从A到B记为:A→B(+1,+4),从B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中B→C( , ),C→ (+1, );
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若图中另有两个格点M,N,且M→A(![]() ,
, ![]() ),M→N(
),M→N(![]() ,
, ![]() ),则N→A应记作 .
),则N→A应记作 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com