
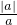 )2012+|2-
)2012+|2- |-
|-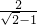 (cot30°-
(cot30°- )0
)0 -
-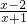 )÷
)÷ 的值.
的值. )-1÷1+2
)-1÷1+2 -1-2(
-1-2( +1)×1
+1)×1 -1-2
-1-2 -2
-2 •
•
 •
•
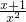 ,
, =1.
=1. )-1÷1+2
)-1÷1+2 -1-2(
-1-2( +1)×1=2+2
+1)×1=2+2 -1-2
-1-2 -2,然后合并即可;
-2,然后合并即可;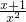 ,再把x2-x-1=0变形得到x2=x+1,最后利用整体代入的方法进行计算.
,再把x2-x-1=0变形得到x2=x+1,最后利用整体代入的方法进行计算.

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com