
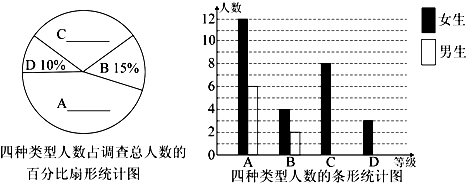
分析 根据B类的人数和所占的百分比求出总人数,再根据A类的人数求出A类所占的百分比,再用1减去A、B、D所占的百分比,求出C类所占的百分比,从而得出C、D类的男生人数,即可补全统计图,再用该校的总人数乘以非常喜欢所占的百分比,求出非常喜欢”马拉松的人数.
解答 解:根据题意得:
$\frac{4+2}{15%}$=40(人),
A类型所占的百分比是:$\frac{12+6}{40}$×100%=45%,
C类型所占的百分比是:1-10%-15%-45%=30%,
C类型的男生人数是:40×30%-8=4(人),
D类型的男生人数是:40×10%-3=1(人),
补图如下: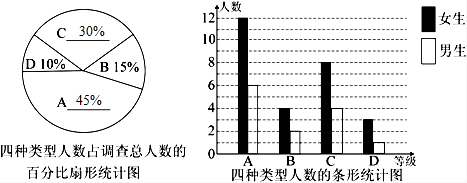
600×45%=270(人),
答:该校600名学生中“非常喜欢”马拉松的人数为270.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从统计图中得到必要的信息,求出A类和C类所占的百分比是解决问题的关键.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源:2016-2017学年江西省下期九年级第一次月考数学试卷(解析版) 题型:判断题
某市推行高效课堂教学改革,已知小红所在的九(2)班有30人,恰好分成5个学习小组(记为A、B、C、D、E).
(1)在李老师的一次随机点名中,求恰好点到小红的概率是多少;
(2)数学老师在某次课堂中设置了2个学习小组的展示成果,请用树形图或列表法求出随机恰好点到A、B学习小组展示成果的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
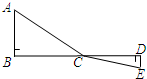 阅读材料:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为$\sqrt{16+(8-x)^{2}}$+$\sqrt{4+{x}^{2}}$.然后利用几何知识可知:当A、C、E在一条直线上时,x=$\frac{8}{3}$时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式$\sqrt{25+(12-x)^{2}}$+$\sqrt{9+{x}^{2}}$的最小值为4$\sqrt{13}$.
阅读材料:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为$\sqrt{16+(8-x)^{2}}$+$\sqrt{4+{x}^{2}}$.然后利用几何知识可知:当A、C、E在一条直线上时,x=$\frac{8}{3}$时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式$\sqrt{25+(12-x)^{2}}$+$\sqrt{9+{x}^{2}}$的最小值为4$\sqrt{13}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com