
【题目】已知两个等腰Rt△ABC,Rt△CEF有公共顶点C,∠ABC﹣∠CEF=90°,连接AF,M是AF的中点
(1)如图1,当CB与CE在同一直线上时,连接CM,若CB=1,CE=2,求CM的长.
(2)如图2,连接MB,ME,当∠BCE=45°时,求证:BM=ME.

【答案】(1)![]() .(2)证明见解析.
.(2)证明见解析.
【解析】
(1)首先利用勾股定理得出AF的长,再利用直角三角形斜边的中线等于斜边的一半来解答即可;(2) 连接BE、DE,先由△ABM≌△FDM,得出AB=DF,BM=DM,进而得出AB=BC=DF,再经过证明△BCE≌△DFE,得出△BDE是等腰直角三角形即可求解.
(1)解:∵△ABC是等腰三角形,CB=1,
∴∠ACB=45°,AC=![]() ,
,

∵△CEF是等腰直角三角形,CE=2
∴∠ECF=45°,CF=2![]() ,
,
∴∠ACF=∠ACB+∠ECF=45°+45°=90°,
∴AF2=AC2+CF2=10,
∵M是AF的中点,
∴CM=![]() AF=
AF=![]() .
.
(2)证明:由此BM交CF于D,连接BE、DE.
∵∠BCE=45°,
∴∠ACD=45°×2+45°=135°,
∴∠BAC+∠ACF=45°+135°=180°,
∴AB∥CF,
∴∠BAM=∠DFM,
∵M是AF的中点,
∴AM=FM,
在△ABM和△FDM中, ,
,
∴△ABM≌△FDM(ASA),
∴AB=DF,BM=DM,
∴AB=BC=DF,
在△BCE和△DFE中, ,
,
∴△BCE≌△DFE(SAS),
∴BE=DE,∠BEC=∠DEF,
∴∠BED=∠BEC+∠CED=∠DEF+∠CED=∠CEF=90°,
∴△BDE是等腰直角三角形,
∵BM=MD,
∴BM=ME=![]() BD,
BD,
∴BM=ME.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,已知AB=6,BC=8,E是边AD上的点,以CE为折痕折叠纸片,使点D落在点F处,连接FC,当△AEF为直角三角形时,DE的长为_________.
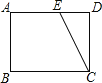
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为y米,乙行驶的时间为x秒,y与x之间的关系如图所示.甲到达目的地时,乙距目的地还有_____米.
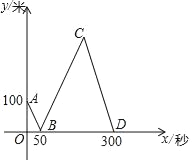
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区计划对面积为3600m2的区域进行绿化,经投标,由甲,乙两个工程队来完成,已知甲队4天能完成绿化的面积等于乙队8天完成绿化的面积,甲队3天能完成绿化的面积比乙队5天能完成绿化面积多50m2
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)若甲队每天化费用是1.2万元,乙队每天绿化费用为0.5万元,要使这次绿化的总费用不超过40万元,则至少应安排乙工程队绿化多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的是____________________________
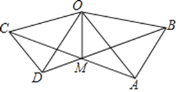
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机给学生带来方便的同时也带来了很大的影响.常德市某校初一年级在一次家长会上对若干家长进行了一次对“学生使用手机”现象看法的调查,将调查数据整理得如下统计图(A:绝对弊大于利,B:绝对利大于弊,C:相对弊大于利,D:相对利大于弊):

(1)这次调查的家长总人数为多少人?表示“C相对弊大于利”的家长人数为多少人?
(2)本次调查的家长中表示“B绝对利大于弊”所占的百分比是多少?并补全条形统计图.
(3)求扇形统计图图2中表示“A:绝对弊大于利”的扇形的圆心角度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() ,点
,点![]() 在
在![]() 轴上,将三角形
轴上,将三角形![]() 沿
沿![]() 轴负方向平移,平移后的图形为三角形
轴负方向平移,平移后的图形为三角形![]() ,且点
,且点![]() 的坐标为
的坐标为![]() .
.
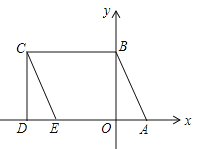
(1)直接写出点![]() 的坐标为 ;
的坐标为 ;
(2)在四边形![]() 中,点
中,点![]() 从点
从点![]() 出发,沿“
出发,沿“![]() ”移动,若点
”移动,若点![]() 的速度为每秒1个单位长度,运动时间为
的速度为每秒1个单位长度,运动时间为![]() 秒,回答下问题:
秒,回答下问题:
①求点![]() 在运动过程中的坐标(用含
在运动过程中的坐标(用含![]() 的式子表示,写出过程);
的式子表示,写出过程);
②当![]() 秒时,点
秒时,点![]() 的横坐标与纵坐标互为相反数;
的横坐标与纵坐标互为相反数;
③当![]() 秒
秒![]() 秒时,设
秒时,设![]() ,
,![]() ,
,![]() ,试问
,试问![]() 之间的数量关系能否确定?若能,请用含
之间的数量关系能否确定?若能,请用含![]() 的式子表式
的式子表式![]() ,写出过程;若不能,说明理由.
,写出过程;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,………按这样的规律进行下去,正方形A2018B2018C2018C2017的面积为( )
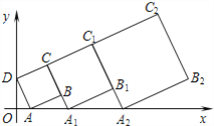
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com