
分析 设方程的另一个根为x2,根据韦达定理列方程组求解可得.
解答 解:设方程的另一个根为x2,
则$\left\{\begin{array}{l}{2+\sqrt{3}+{x}_{2}=3}\\{(2+\sqrt{3}){x}_{2}=\frac{c}{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{2}=1-\sqrt{3}}\\{c=-2-2\sqrt{3}}\end{array}\right.$,
答:方程的另一个根为1-$\sqrt{3}$,c的值为-2-2$\sqrt{3}$.
点评 本题主要考查根与系数的关系,熟练掌握韦达定理是解题的关键.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
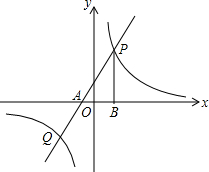 如图,经过点A(-1,0)的一次函数y=ax+b(a≠0)与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=2,点Q的坐标为(-3,m)
如图,经过点A(-1,0)的一次函数y=ax+b(a≠0)与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=2,点Q的坐标为(-3,m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
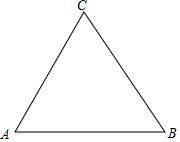 如图,等边三角形ABC为一花坛,现要将其改为圆形花坛覆盖在△ABC上,且使其占地面积最小.
如图,等边三角形ABC为一花坛,现要将其改为圆形花坛覆盖在△ABC上,且使其占地面积最小.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
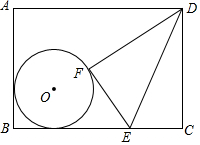 如图,圆O在矩形ABCD内,且与AB,BC边都相切,E是BC上一点,将△DCE延DE翻折,点C的对称点F恰好落在圆O上.已知AB=20,BC=26,CE=10,则圆O的半径为5.
如图,圆O在矩形ABCD内,且与AB,BC边都相切,E是BC上一点,将△DCE延DE翻折,点C的对称点F恰好落在圆O上.已知AB=20,BC=26,CE=10,则圆O的半径为5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{276}{35}$ | B. | -$\frac{276}{35}$ | C. | $\frac{11}{12}$ | D. | -$\frac{11}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com