
【题目】如图,E、F分别是AD和BC上的两点,EF将四边形ABCD分成两个边长为5cm的正方形,∠DEF=∠EFB=∠B=∠D=90°;点H是CD上一点且CH=lcm,点P从点H出发,沿HD以lcm/s的速度运动,同时点Q从点A出发,沿A→B→C以5cm/s的速度运动.任意一点先到达终点即停止运动;连结EP、EQ.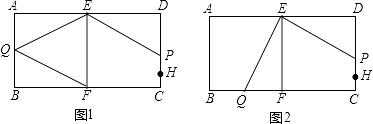
(1)用t表示△EPD的面积;
(2)试探究:当t为何值时,△EPD的面积等于△EQF面积的 ![]() ?
?
【答案】
(1)(10﹣2.5t)cm2
(2)
解:分三种情况讨论:
①如图1所示,过Q作QM⊥EF,垂足为M.

∵四边形ABFE是正方形,
∴QM=AE=5cm.
当0<t≤1时,S△EQF= ![]() EF×QM=
EF×QM= ![]() ×5×5=12.5,S△EPD=
×5×5=12.5,S△EPD= ![]() ED×DP=
ED×DP= ![]() ×5×(4﹣t)=10﹣2.5t,
×5×(4﹣t)=10﹣2.5t,
当 ![]() S△EQF=S△EPD时,即
S△EQF=S△EPD时,即 ![]() ×12.5=10﹣2.5t,
×12.5=10﹣2.5t,
解得,t=0.5;
②当1<t≤2时,S△EQF= ![]() ×EF×FQ=2.5FQ,S△EPD=
×EF×FQ=2.5FQ,S△EPD= ![]() ED×DP=
ED×DP= ![]() ×5×(4﹣t)=10﹣2.5t,
×5×(4﹣t)=10﹣2.5t,

∵FQ=10﹣5t,
∴ ![]() ×2.5(10﹣5t)=10﹣2.5t,
×2.5(10﹣5t)=10﹣2.5t,
解得:t=1.2;
③当2<t≤3时,S△EQF= ![]() FQ×EF=2.5(5t﹣10),S△EPD=
FQ×EF=2.5(5t﹣10),S△EPD= ![]() ED×DP=
ED×DP= ![]() ×5×(4﹣t)=10﹣2.5t,
×5×(4﹣t)=10﹣2.5t,

∴ ![]() ×2.5×(5t﹣10)=2.5(4﹣t),
×2.5×(5t﹣10)=2.5(4﹣t),
解得:t= ![]() ;
;
综上所述:当t的值为0.5s或1.2s或 ![]() s时,△EPD的面积等于△EQF面积的
s时,△EPD的面积等于△EQF面积的 ![]() .
.
【解析】解:(1)S△EPD= ![]() ED×DP=
ED×DP= ![]() ×5×(4﹣t)=10﹣2.5t;所以答案是:(10﹣2.5t)cm2;
×5×(4﹣t)=10﹣2.5t;所以答案是:(10﹣2.5t)cm2;
【考点精析】通过灵活运用三角形的面积,掌握三角形的面积=1/2×底×高即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD、EF相交于点O . 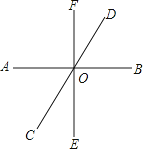
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组 ![]() (实数m是常数).
(实数m是常数).
(1)若x+y=1,求实数m的值;
(2)若﹣1≤x﹣y≤5,求m的取值范围;
(3)在(2)的条件下,化简:|m+2|+|2m﹣3|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程变形属于移项的是( )
A.由﹣2y﹣5=﹣1+y,得﹣2y﹣y=5﹣1
B.由﹣3x=﹣6,得x=2
C.由 ![]() y=2,得y=10
y=2,得y=10
D.由﹣2(1﹣2x)+3=0,得﹣2+4x+3=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使用计算器计算各式:6×7= 42 ,66×67= 4422 ,666×667= 444222 ,6 666×6 667= 44442222 .
(1)根据以上结果,你发现了什么规律?
(2)依照你发现的规律,不用计算器,你能直接写出666 666×666 667的结果吗?请你试一试.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:

(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A、B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com