
【题目】完成下面的证明:
如图,已知∠1、∠2互为补角,且∠3=∠B,
求证:∠AED=∠ACB.
证明:∵∠1+∠2=180°,∠2+∠4=180°
∴∠1=∠4 (______)
∴AB∥EF(_______)
∴∠3=______(______)
又∠3=∠B
∴∠B=_______(_______)
∴DE∥BC (________)
∴∠AED=∠ACB (_______)

【答案】等式基本性质;内错角相等,两直线平行;∠ADE;两直线平行,内错角相等;∠ADE;等量代换;同位角相等,两直线平行;两直线平行,同位角相等.
【解析】
根据等式的基本性质、平行线的判定和性质以及等量代换进行推理填空即可.
证明:∵∠1+∠2=180°,∠2+∠4=180°,
∴∠1=∠4 (等式基本性质),
∴AB∥EF(内错角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等),
又∠3=∠B,
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠ACB (两直线平行,同位角相等),
故答案为:等式基本性质;内错角相等,两直线平行;∠ADE;两直线平行,内错角相等;∠ADE;等量代换;同位角相等,两直线平行;两直线平行,同位角相等.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图1,将一块含![]() 角的三角板ABO的一边BO放在直线MN上,AB边在直线MN的上方,其中
角的三角板ABO的一边BO放在直线MN上,AB边在直线MN的上方,其中![]() ,另一块含
,另一块含![]() 角的三角板POQ的一边OQ在直线MN上,另一边OP在直线MN的下方.
角的三角板POQ的一边OQ在直线MN上,另一边OP在直线MN的下方.

![]() 现将图1中的三角板POQ绕点O按顺时针方向旋转,当直线MN恰好为
现将图1中的三角板POQ绕点O按顺时针方向旋转,当直线MN恰好为![]() 的平分线时,如图2所示,则
的平分线时,如图2所示,则![]() 的度数______度;
的度数______度;
![]() 继续将图2中的三角板绕点O按顺时针方向旋转至图3的位置,使得边OA落在
继续将图2中的三角板绕点O按顺时针方向旋转至图3的位置,使得边OA落在![]() 的内部,且AO恰好为
的内部,且AO恰好为![]() 的平分线时,求
的平分线时,求![]() 的度数;
的度数;
![]() 在上述直角三角板从图1按顺时针方向旋转至图位置为止,这个过程中,若三角板POQ绕点O以每秒
在上述直角三角板从图1按顺时针方向旋转至图位置为止,这个过程中,若三角板POQ绕点O以每秒![]() 的速度匀速旋转,当三角板POQ的OP边或OQ边所在直线平分
的速度匀速旋转,当三角板POQ的OP边或OQ边所在直线平分![]() ,则求此时三角板POQ绕点O旋转的时间t的值
,则求此时三角板POQ绕点O旋转的时间t的值![]() 请直接写出答案
请直接写出答案![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一块直角三角板![]() 放置在锐角
放置在锐角![]() 上,使得该三角板的两条直角边
上,使得该三角板的两条直角边![]() 恰好分别经过点
恰好分别经过点![]()
(1)如图①,若![]() 时,点
时,点![]() 在
在![]() 内,则
内,则![]() 度,
度,![]() ____度,
____度,![]() 度;
度;
(2)如图②,改变直角三角板![]() 的位置,使点
的位置,使点![]() 在
在![]() 内,请探究
内,请探究![]() 与
与![]() 之间存在怎样的数量关系,并验证你的结论;
之间存在怎样的数量关系,并验证你的结论;
(3)如图③,改变直角三角板![]() 的位置,使点
的位置,使点![]() 在
在![]() 外,且在
外,且在![]() 边的左侧,直接写出
边的左侧,直接写出![]() 三者之间存在的数量关系.
三者之间存在的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的10张卡片上分别写有11至20十个数字,将它们背面朝上洗匀后,任意抽一张,将下列事件发生的机会的大小填在横线上.
![]()
(1)P1(抽到数字11)=_______;
(2)P2(抽到两位数)=_______,P3(抽到一位数)=_______;
(3)P4(抽到的数大于10)=_______,P5(抽到的数大于16)=_______,P6(抽到的数小于16)=_______;
(4)P7(抽到的数是2的倍数)=_______,P8(抽到的数是3的倍数)=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.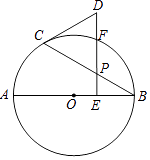
(1)求证:DC是⊙O的切线;
(2)若∠CBA=30°,射线EP交⊙O于点 F,当点 F恰好是弧BC的中点时,判断以B,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑到学校.如果小明跑步的速度均匀的,到达小彬家用了8分钟,整个跑步过程用时共32分钟.
(1)以小明家为原点、向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家;
(2)用点C表示出学校的位置;
(3)求小彬家与学校之间的距离.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com