
 已知:如图,在矩形ABCD中,AB=3,点E在AB的延长线上,且AE=AC,联结CE,取CE的中点F,联结BF、DF.
已知:如图,在矩形ABCD中,AB=3,点E在AB的延长线上,且AE=AC,联结CE,取CE的中点F,联结BF、DF.分析 (1)方法一:如图1中,连接AF,只要证明△ABF≌DCF即可.方法二:如图2中,连接BD,与AC相交于点O,联结OF,只要证明OB=OF=OD即可.
(2)由y=DF=$\sqrt{B{D}^{2}-B{F}^{2}}$即可解决问题.
(3)首先证明CE=DF=AF,列出方程即可解决.
解答 (1)证明:方法一:如图1中,连接AF,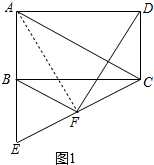
∵AE=AC,点F为CE的中点,
∴AF⊥CE,即∠AFC=90°,
∵在矩形ABCD中,AB=CD,∠ABC=∠DCB=90°,
∴∠CBE=180°-∠ABC=90°,
∴EF=BF=CF=$\frac{1}{2}CE$,
∴∠FBC=∠FCB,即∠ABC+∠FBC=∠DCB+∠FCB,
∴∠ABF=∠DCF,
在△ABF和△DCF中,
$\left\{\begin{array}{l}{BF=CF}\\{∠ABF=∠DCF}\\{AB=CD}\end{array}\right.$,
∴△ABF≌DCF,
∴∠AFB=∠DFC,
∴∠BFD=∠AFB+∠AFD=∠AFD+∠DFC=∠AFC=90°,
即DF⊥BF;
方法二:如图2中,连接BD,与AC相交于点O,联结OF,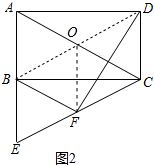
∵在矩形ABCD中,AC=BD,OA=OC,OB=OD,
∴OA=OC=OB=OD=$\frac{1}{2}$AC=$\frac{1}{2}$BD,
∵点F是CE的中点,∴OF=$\frac{1}{2}$AE,
∵AE=AC,∴OF=$\frac{1}{2}$AC=$\frac{1}{2}$BD,
∴OF=OB=OD,
∴∠OBF=∠OFB,∠OFD=∠ODF,
∵∠OBF+∠OFB+∠OFD+∠ODF=180°,
∴2∠OFB+2∠OFD=180°,
∴∠OFB+∠OFD=90°,即∠BFD=90°,∴DF⊥BF;
(2)解:在Rt△ABC中,BC2=AC2-AB2=x2-9,
∵AE=AC=x,∴BE=x-3,
∴EC=$\sqrt{B{C}^{2}+B{E}^{2}}$=$\sqrt{({x}^{2}-9)+(x-3)^{2}}$=$\sqrt{2{x}^{2}-6x}$,
∴BF=$\frac{1}{2}CE$=$\frac{{\sqrt{2{x^2}-6x}}}{2}$,
∴y=DF=$\sqrt{B{D}^{2}-B{F}^{2}}$=$\sqrt{{x}^{2}-\frac{2{x}^{2}-6x}{4}}$=$\frac{{\sqrt{2{x^2}+6x}}}{2}$,
∴y=$\frac{\sqrt{2{x}^{2}+6x}}{2}$(x>3).
(3)∵△ABF≌DCF,∴AF=DF,
∵在Rt△ABC中,CE=2BF,又∵DF=2BF,∴CE=DF=AF,
∴$\sqrt{2{x^2}-6x}$=$\frac{{\sqrt{2{x^2}+6x}}}{2}$,
∴x1=0,x2=5.经检验,x1=0,x2=5都是方程的根,但x=0不符合题意.
∴BC=$\sqrt{{x}^{2}-9}$=$\sqrt{{5}^{2}-{3}^{2}}$=4.
点评 本题考查四边形综合题、矩形的性质、全等三角形的判定和性质勾股定理等知识,解题的关键是灵活应用这些知识解决问题,学会构建方程解决问题,属于中考压轴题.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案科目:初中数学 来源: 题型:选择题
| A. | y2-3y-4=y(y-3)-4 | B. | 1-4x+4x2=(1-2x)2 | C. | x2+y2=(x+y)(x-y) | D. | x-1=x(1-$\frac{1}{x}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x2-7=3y+1 | B. | $\frac{\sqrt{7}}{3}$x-$\sqrt{5}$=$\frac{{x}^{2}}{2}$+x | C. | 5x2-6y-2=0 | D. | ax2+bx+c=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2 | B. | (x+6)2 | C. | (x+2)(x-6) | D. | (x+2)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是江津区某一天的气温随时间变化的图象,根据图象回答:在这一天中:
如图是江津区某一天的气温随时间变化的图象,根据图象回答:在这一天中:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com