
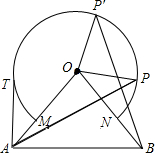
 如图,△OAB中,OA=OB=10,∠AOB=70°,以点O为圆心,6为半径的优弧$\widehat{MN}$分别交OA、OB于点M,N.
如图,△OAB中,OA=OB=10,∠AOB=70°,以点O为圆心,6为半径的优弧$\widehat{MN}$分别交OA、OB于点M,N.分析 (1)首先根据已知得出∠AOP=∠BOP′,进而得出△AOP≌△BOP′,即可得出答案;
(2)利用切线的性质得出∠ATO=90°,再利用勾股定理求出AT的长,进而得出TH的长即可得出答案;
(3)当OQ⊥OA时,△AOQ面积最大,且左右两半弧上各存在一点分别求出即可.
解答 (1)证明:如图1,∵∠AOP=∠AOB+∠BOP=80°+∠BOP,
∠BOP′=∠POP′+∠BOP=80°+∠BOP,
∴∠AOP=∠BOP′,
∵在△AOP和△BOP′中
$\left\{\begin{array}{l}{OA=OB}\\{∠AOP=∠BOP′}\\{OP=OP′}\end{array}\right.$,
∴△AOP≌△BOP′(SAS),
∴AP=BP′;
(2)解:如图1,连接OT,过点T作TH⊥OA于点H,
∵AT是⊙O的切线,
∴∠ATO=90°,
∴AT=$\sqrt{O{A}^{2}-O{T}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵$\frac{1}{2}$×OA×TH=$\frac{1}{2}$×AT×OT,
即$\frac{1}{2}$×10×TH=$\frac{1}{2}$×8×6,
解得:TH=$\frac{24}{5}$,即点T到OA的距离为$\frac{24}{5}$;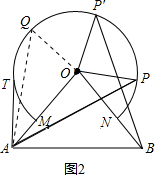
(3)解:如图2,当OQ⊥OA时,△AOQ的面积最大;
理由:∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大,
∴∠BOQ=∠AOQ+∠AOB=90°+70°=160°,
当Q点在优弧$\widehat{MN}$右侧上,
∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大,
∴∠BOQ=∠AOQ-∠AOB=90°-70°=20°,
综上所述:当∠BOQ的度数为20°或160°时,△AOQ的面积最大.
点评 本题考查了圆的综合题、切线的判定与性质、全等三角形的判定与性质,第二个问题的关键是利用面积法求出线段TH,第三个问题的关键是学会用分类讨论的思想思考问题,注意一题多解,属于中考压轴题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第2个正方形ACEF,再以对角线AE为边作第3个正方形AEGH,如此下去…,记正方形ABCD的面积S1=1,按上述方法所作的正方形的面积依次为S2,S3…,Sn,则Sn=( )
如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第2个正方形ACEF,再以对角线AE为边作第3个正方形AEGH,如此下去…,记正方形ABCD的面积S1=1,按上述方法所作的正方形的面积依次为S2,S3…,Sn,则Sn=( )| A. | 2n-1 | B. | 2n | C. | 2n+1 | D. | 2n+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com