
【题目】如图,AB是⊙O的弦,C是劣弧 ![]() 的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2.
的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2. 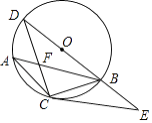
(1)求CB的长;
(2)延长DB到E,使BE=OB,连接CE,求证:CE是⊙O的切线.
【答案】
(1)解:∵C是劣弧 ![]() 的中点,
的中点,
∴∠1=∠2,
∵∠1=∠D,
∴∠2=∠D,
∵∠BCF=∠DCB,
∴△BCF∽△DCB,
∴ ![]() ,
,
∴BC2=CFCD=1×3=3,
∴BC= ![]() ;
;
(2)解:∵BD是⊙O的直径,
∴∠BCD=90°,
∴BD2=BC2+CD2=12,
∴BD=2 ![]() ,
,
∴OB=BE=BC,
连接OC,

∴∠OCE=90°,
∴OC⊥CE,
∴CE是⊙O的切线.
【解析】(1)由C是劣弧 ![]() 的中点,得到∠1=∠2,等量代换得到∠2=∠D,根据相似三角形的性质即可得到结论;(2)由BD是⊙O的直径,得到∠BCD=90°,根据勾股定理得到BD=2
的中点,得到∠1=∠2,等量代换得到∠2=∠D,根据相似三角形的性质即可得到结论;(2)由BD是⊙O的直径,得到∠BCD=90°,根据勾股定理得到BD=2 ![]() ,证得OB=BE=BC,连接OC,推出OC⊥CE,即可得到结论.
,证得OB=BE=BC,连接OC,推出OC⊥CE,即可得到结论.
【考点精析】掌握切线的判定定理和相似三角形的判定与性质是解答本题的根本,需要知道切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】现要把192吨物资从我市运往甲、乙两地,用大、小两种货车共18辆恰好能一次性运完这批物资.已知这两种货车的载重量分别为14吨/辆和8吨/辆,运往甲、乙两地的运费如表:
运往地 | 甲地(元/辆) | 乙地(元/辆) |
大货车 | 720 | 800 |
小货车 | 500 | 650 |
(1)求这两种货车各用多少辆?
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式;
(3)在(2)的条件下,若运往甲地的物资部少于96吨,请你设计出使总运费最低的货车调配方案,并求出最少总运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A 和 B 两地在一条河的两岸,现要在河上造一座桥 MN.桥造在何处才能使从 A 到 B 的路径 AMNB 最短?在下图中画出路径,不写画法但要说明理由.(假定河的两岸是平行的直线,桥要与河垂直.)
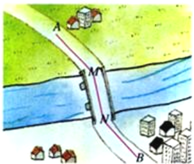
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、F、C、E在同一条直线上,点A、D在直线BC的异侧,AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)若∠BFD=150°,求∠ACB的度数.
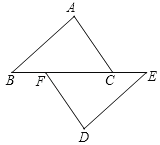
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:若关于x的一元一次方程ax=b的解为b+a,则称该方程为“和解方程”. 例如:方程2x=﹣4的解为x=﹣2,而﹣2=﹣4+2,则方程2x=﹣4为“和解方程”.
请根据上述规定解答下列问题:
(1)已知关于x的一元一次方程3x=m是“和解方程”,求m的值;
(2)已知关于x的一元一次方程﹣2x=mn+n是“和解方程”,并且它的解是x=n,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过原点的直线y=k1x和y=k2x与反比例函数y= ![]() 的图象分别交于两点A,C和B,D,连接AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连接AB,BC,CD,DA.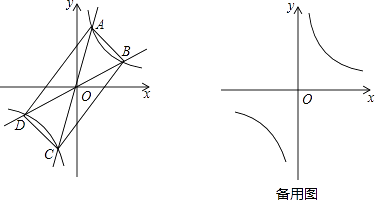
(1)四边形ABCD一定是四边形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时k1 , k2之间的关系式;若不能,说明理由;
(3)设P(x1 , y1),Q(x2 , y2)(x2>x1>0)是函数y= ![]() 图象上的任意两点,a=
图象上的任意两点,a= ![]() ,b=
,b= ![]() ,试判断a,b的大小关系,并说明理由.
,试判断a,b的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应珠海环保城市建设,我市某污水处理公司不断改进污水处理设备,新设备每小时处理污水量是原系统的1.5倍,原来处理1200m3污水所用的时间比现在多用10小时.
(1)原来每小时处理污水量是多少m2?
(2)若用新设备处理污水960m3,需要多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l与⊙O相离,过点O作OA⊥l,垂足为A,OA交⊙O于点B,点C在直线l上,连接CB并延长交⊙O于点D,在直线l上另取一点P,使∠PCD=∠PDC. 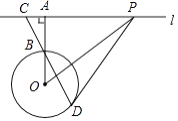
(1)求证:PD是⊙O的切线;
(2)若AC=1,AB=2,PD=6,求⊙O的半径r和△PCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
如图,∠AOB=90°,∠COD=90°,OA平分∠DOE,若∠BOC=20°,求∠COE的度数
解:因为∠AOB=90°.
所以∠BOC+∠AOC=90°
因为∠COD=90°
所以∠AOD+∠AOC=90°.
所以∠BOC=∠AOD. ( )
因为∠BOC=20°.
所以∠AOD=20°.
因为OA平分∠DOE
所以∠ =2∠AOD= °. ( )
所以∠COE=∠COD﹣∠DOE= °

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com