
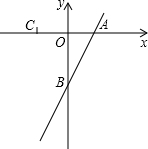
| OB |
| OA |
|
|
4
| ||
| 5 |
| 4 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
| 8 |
| 5 |
| 6 |
| 5 |
| 8 |
| 5 |
| 6 |
| 5 |
| 8 |
| 5 |


科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
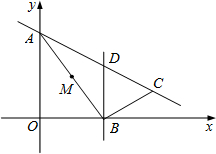 点B按顺时针方向旋转90°,得到线段BC.过点B作x轴的垂线交直线AC于点D.设点B坐标是(t,0).
点B按顺时针方向旋转90°,得到线段BC.过点B作x轴的垂线交直线AC于点D.设点B坐标是(t,0).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 3 |
| 3 |
| 3 |
| 3 |
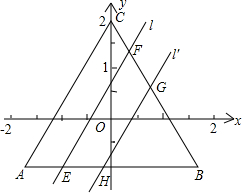 是否改变?若不变,请指出来;若改变,请写出面积变化的范围.(不必说明理由)
是否改变?若不变,请指出来;若改变,请写出面积变化的范围.(不必说明理由)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 运动鞋 价格 | 甲 | 乙 |
| 进价(元/双) | m | m-20 |
| 售价(元/双) | 240 | 160 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 月份 | 用水量(m3) | 水费(元) |
| 5 | 5 | 7.5 |
| 6 | 9 | 27 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com