
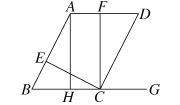
【题目】如图,已知AB∥CD,AD∥BC,∠DCE=90°,点E在线段AB上,∠FCG=90°,点F在直线AD上,∠AHG=90°.
(1)找出图中与∠D相等的角,并说明理由;
(2)若∠ECF=25°,求∠BCD的度数;
(3)在(2)的条件下,点C(点C不与B,H两点重合)从点B出发,沿射线BG的方向运动,其他条件不变,求∠BAF的度数.
【答案】(1)与∠D相等的角为∠DCG,∠ECF,∠B(2)155°(3)25°或155°
【解析】
(1)根据平行线性质和同角的余角相等可得:与∠D相等的角为∠DCG,∠ECF,∠B.
(2)由垂直定义得∠FCD=65°,所以∠BCD=65°+90°=155°.
(3)分两种情况进行讨论:①如图a,当点C在线段BH上时,点F在DA的延长线上, 由AD∥BC,得∠BAF=∠B;②如图b,当点C在BH的延长线上时,点F在线段AD上.∠B=25°,AD∥BC,所以∠BAF=180°-25°=155°.
解:(1)与∠D相等的角为∠DCG,∠ECF,∠B.(1分)理由如下:
∵AD∥BC,
∴∠D=∠DCG.
∵∠FCG=90°,∠DCE=90°,
∴∠ECF=∠DCG=∠D.
∵AB∥DC,
∴∠B=∠DCG=∠D,
∴与∠D相等的角为∠DCG,∠ECF,∠B.
(2)∵∠ECF=25°,∠DCE=90°,
∴∠FCD=65°.
又∵∠BCF=90°,
∴∠BCD=65°+90°=155°.
(3)分两种情况进行讨论:
①如图a,当点C在线段BH上时,点F在DA的延长线上,此时∠ECF=∠DCG=∠B=25°.
∵AD∥BC,
∴∠BAF=∠B=25°;
②如图b,当点C在BH的延长线上时,点F在线段AD上.
∵∠B=25°,AD∥BC,
∴∠BAF=180°-25°=155°.
综上所述,∠BAF的度数为25°或155°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,点D是⊙O上的一点,点C是 ![]() 的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°.
的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°. 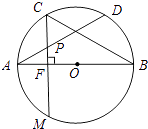
(1)求∠ABC的度数;
(2)若CM=4 ![]() ,求
,求 ![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△AOB,AO=AB=5,OB=6.以O为原点,以OB边所在的直线为x轴,以垂直于OB的直线为y轴建立平面直角坐标系.
(1)求点A的坐标;
(2)若点A关于y轴的对称点为M,点N的横、纵坐标之和等于点A的横坐标,请在图中画出一个满足条件的△AMN,并直接在图上标出点M,N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F分别是AB,CD上的点,点G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列判断中,错误的是( )

A. ∠AEF=∠EFC B. ∠A=∠BCF C. ∠AEF=∠EBC D. ∠BEF+∠EFC=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(n,-2),B(1,4)是一次函数 y=kx+b的图象和反比例函数 ![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
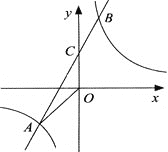
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)观察图象,直接写出反比例函数值大于一次函数值x取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副含 ![]() 和
和 ![]() 角的三角板
角的三角板 ![]() 和
和 ![]() 叠合在一起,边
叠合在一起,边 ![]() 与
与 ![]() 重合,
重合, ![]() (如图1),点
(如图1),点 ![]() 为边
为边 ![]()
![]() 的中点,边
的中点,边 ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,此时线段
,此时线段 ![]() 的长是 . 现将三角板
的长是 . 现将三角板 ![]() 绕点
绕点 ![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在 ![]() 从
从 ![]() 到
到 ![]() 的变化过程中,点
的变化过程中,点 ![]() 相应移动的路径长共为 . (结果保留根号)
相应移动的路径长共为 . (结果保留根号)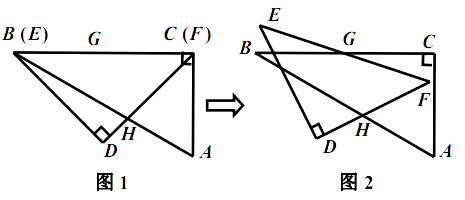
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两点在数轴上对应的数分别为a,b,且点A在点B的左边,|a|=10,a+b=80,ab<0.
(1)求出a,b的值;
(2)现有一只电子蚂蚁P从点A出发,以3个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q从点B出发,以2个单位长度/秒的速度向左运动.
①设两只电子蚂蚁在数轴上的点C相遇,求出点C对应的数是多少?
②经过多长时间两只电子蚂蚁在数轴上相距20个单位长度?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com