
【题目】已知关于 x 的方程 x2-(2k+1)x+k2+2k=0,有两个实数根 x1,x2.
(1)求 k 的取值范围;
(2)若方程的两实数根 x1,x2 满足 x1x2-x12-x22=-16,求实数 k 的值.
【答案】(1)![]() ;(2)k=-3
;(2)k=-3
【解析】
(1)利用判别式的意义得到△=(2k+1)2-4(k2+2k)≥0,然后解不等式得到k的范围;
(2)据题根与系数的关系得到x1+x2=2k+1,x1x2=k2+2k,再利用x1x2-x12-x22=-16得到-(x1+x2)2+3x1x2=-16,则-(2k+1)2+3(k2+2k)=-16,然后解关于k的方程得到满足条件的k的值.
解:(1)由题意得△=(2k+1)2-4(k2+2k)≥0,
解得:![]()
(2)根据题意得x1+x2=2k+1,x1x2=k2+2k,
∵x1x2-x12-x22=-16,
∴x1x2-[(x1+x2)2-2x1x2]=-16,即-(x1+x2)2+3x1x2=-16,
∴-(2k+1)2+3(k2+2k)=-16,
整理得k2-2k-15=0,解得k1=5,k2=-3,
∵![]()
∴k=-3


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
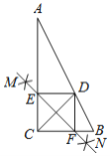
【题目】如图,Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,按下列步骤作图:
步骤1:分别以点C和点D为圆心,大于![]() 的长为半径作弧,两弧相交于M,N两点;
的长为半径作弧,两弧相交于M,N两点;
步骤2:作直线MN,分别交AC,BC于点E,F;
步骤3:连接DE,DF.
若AC=4,BC=2,则线段DE的长为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=ax2+bx+c,其中 y 与 x 的部分对应值如表:
x | -2 | -1 | 0.5 | 1.5 |
y | 5 | 0 | -3.75 | -3.75 |
下列结论正确的是( )
A.abc<0B.4a+2b+c>0
C.若 x<-1 或 x>3 时,y>0D.方程 ax2+bx+c=5 的解为 x1=-2,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,折叠矩形纸片 ABCD,具体操作:①点 E 为 AD 边上一点(不与点 A,D 重合),把△ABE 沿 BE 所在的直线折叠,A 点的对称点为 F 点;②过点 E 对折∠DEF,折痕EG 所在的直线交 DC 于点 G,D 点的对称点为 H 点.
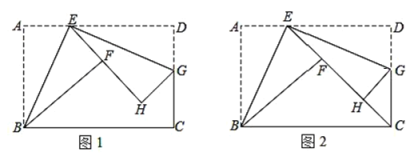
(1)求证:△ABE∽△DEG.
(2)若 AB=6,BC=10
①点 E 在移动的过程中,求 DG 的最大值;
②如图 2,若点 C 恰在直线 EF 上,连接 DH,求线段 DH 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长、宽均为![]() 米的十字路口,现遇到红灯,有
米的十字路口,现遇到红灯,有![]() 辆车依次呈一直线停在路口的交通白线后,每二辆车间隔为
辆车依次呈一直线停在路口的交通白线后,每二辆车间隔为![]() 米每辆车长
米每辆车长![]() 米.每辆车的速度
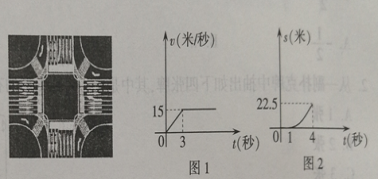
米.每辆车的速度![]() (米/秒)关于时间(秒)的函数(如图1)所示,当绿灯亮起第一辆车的车头与交通白线的距离
(米/秒)关于时间(秒)的函数(如图1)所示,当绿灯亮起第一辆车的车头与交通白线的距离![]() (米)关于时间(秒)的丽数解析式为
(米)关于时间(秒)的丽数解析式为![]() ,如图2所示.当前车启动后,后面一辆车在
,如图2所示.当前车启动后,后面一辆车在![]() 秒后也启动.
秒后也启动.
![]() 求
求![]() 的值.
的值.
![]() 当
当![]() 时,求第一辆车的车头与交通白线的距离
时,求第一辆车的车头与交通白线的距离![]() (米)关于时间(秒)的函数解析式.
(米)关于时间(秒)的函数解析式.
![]() 当
当![]() 时,求第.辆车和第一辆车在这个十字路口中的最大间距(第一辆车的车尾和第二辆车的车头哦).
时,求第.辆车和第一辆车在这个十字路口中的最大间距(第一辆车的车尾和第二辆车的车头哦).
![]() 绿灯持续时间至少要设置多长才能保证在绿灯期间这十辆车都能通过交通白线.
绿灯持续时间至少要设置多长才能保证在绿灯期间这十辆车都能通过交通白线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BC,垂足为E,若BD=![]() ,BC=6,则AB=( )
,BC=6,则AB=( )

A.![]() B.2C.
B.2C.![]() D.3
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com