
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源:同步轻松练习 九年级 数学 上 题型:038
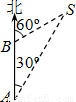
某军舰以20海里/时的速度由西向东航行,一艘电子侦察船以30海里/时的速度由南向北航行.如图,它能侦察出周围50海里(包括50海里)范围内的目标.当军舰行至A处时,电子侦察船正位于A处正南方向的B处,且AB=90海里,如果军舰和侦察船仍按原速度沿原方向继续航行,那么航行途中侦察船能否侦察到这艘军舰?如果能,最早何时能侦察到;如果不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com