
【题目】如图,Rt△ABC中,∠ACB=90°,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:①GA=GP;②∠DCP=45°;③BP垂直平分CE;④GF+ FC =GA;其中正确的判断有______________.(填序号)

【答案】①②③④;
【解析】①∵AP平分∠BAC,∴∠CAP=∠BAP,
∵PG∥AD,∴∠APG=∠CAP,∴∠APG=∠BAP,∴GA=GP;
②∵AP平分∠BAC,∴P到AC,AB的距离相等,
∵BP平分∠CBE,∴P到BC,AB的距离相等,
∴P到AC,BC的距离相等,
∴CP平分∠BCD,∴∠DCP=45°;
③∵BE=BC,BP平分∠CBE,∴BP垂直平分CE(三线合一);
④∵∠BAC与∠CBE的平分线相交于点P,可得点P也位于∠BCD的平分线上,
∴∠DCP=∠BCP,
又PG∥AD,∴∠FPC=∠DCP,∴FP=FC,
∴GF+FC=GF+FP=GP=AG,
故①②③④都正确,
故答案为:①②③④.


科目:初中数学 来源: 题型:
【题目】“成自”高铁自贡仙市段在建设时,甲、乙两个工程队计划参与该项工程建设,甲队单独施工30天完成该项工程的![]() ,这时乙队加入,两队还需同时施工30天,才能完成该项工程.
,这时乙队加入,两队还需同时施工30天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过40天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )
A. 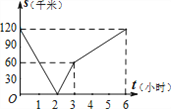 B.
B. 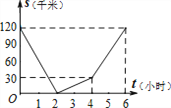
C.  D.
D. 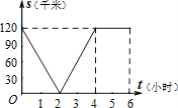
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.

(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线AB: ![]() 交y轴于点A,交x轴于点B,过点E(2,0)作x轴的垂线EF交AB于点D,点P是垂线EF上一点,且S△ADP=2,以PB为边在第一象限作等腰Rt△BPC,则点C的坐标为_________.
交y轴于点A,交x轴于点B,过点E(2,0)作x轴的垂线EF交AB于点D,点P是垂线EF上一点,且S△ADP=2,以PB为边在第一象限作等腰Rt△BPC,则点C的坐标为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社组织一批游客外出旅游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车租金为每辆220元,60座客车租金为每辆300元,问:
(1)这批游客的人数是多少?原计划租用多少辆45座客车?
(2)若租用同一种车,要使每位游客都有座位,应该怎样租用才合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的有()
(1) 钝角的补角一定是锐角
(2) 过己知直线外一点作这条直线的垂线有且只有一条
(3) —个角的两个邻补角是对顶角
(4) 等角的补角相等
(5) 直线![]() 外一点A与直线
外一点A与直线![]() 上各点连接而成的所有线段中,最短线段的长是3cm,则
上各点连接而成的所有线段中,最短线段的长是3cm,则
点A到直线![]() 的距离是3cm .
的距离是3cm .
A. 2个 B. 3个 C. 4 个 D. 5 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数![]() 、
、![]() 我们定义一种新运算
我们定义一种新运算![]() (其中
(其中![]() 、
、![]() 均为非零常数).等式右边是通常的四则运算.由这种运算得到的数我们称之为线性数,记为
均为非零常数).等式右边是通常的四则运算.由这种运算得到的数我们称之为线性数,记为![]() ,其中
,其中![]() 、
、![]() 叫做线性数的一个数对.若实数
叫做线性数的一个数对.若实数![]() 、
、![]() 都取正整数,我们称这样的线性数为正格线性数,这时的
都取正整数,我们称这样的线性数为正格线性数,这时的![]() 、
、![]() 叫做正格线性数的正格数对.
叫做正格线性数的正格数对.
(1)若![]() ,则
,则![]()
![]() .
.
(2)已知![]() ,若正格线性数
,若正格线性数![]() ,求满足不等式组
,求满足不等式组![]() 的所有
的所有![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com