
已知抛物线的顶点(-1,-4)且过点(0,-3),直线l是它的对称轴。
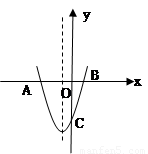
(1)求此抛物线的解析式;
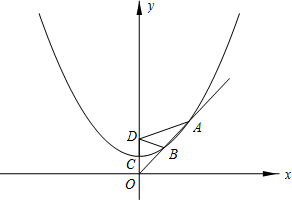
(2)设抛物线交x轴于点A、B(A在B的左边),交y轴于点C,P为l上的一动点,当△PBC的周长最小时,求P点的坐标。
(3)在直线l上是否存在点M,使△MBC是等腰三角形,若存在,直接写出符合条件的点M的坐标;若不存在请说明理由。
(1)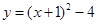 (2)
(2)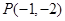 (3)
(3)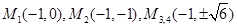
【解析】
试题分析:(1)抛物线的顶点(-1,-4),则设抛物线的顶点式为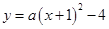 ,因为抛物线过点(0,-3),所以
,因为抛物线过点(0,-3),所以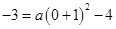 ,解得a=1,所以抛物线的解析式
,解得a=1,所以抛物线的解析式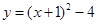
(2)由(1)知抛物线的解析式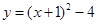
∵直线l是它的对称轴
∴它的对称轴x=-1
抛物线交x轴于点A、B(A在B的左边),令y=0,则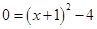 ,解得x=-3,x=1,所以A点的坐标(-3,0),B点的坐标(1,0);抛物线交y轴于点C,令x=0,则
,解得x=-3,x=1,所以A点的坐标(-3,0),B点的坐标(1,0);抛物线交y轴于点C,令x=0,则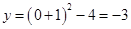 ,所以C点的坐标(0,-3);P为l上的一动点,当△PBC的周长=PB+PC+BC,因为BC的长度一定,所以要使△PBC的周长最小,即PB+PC最小,作点B关于对称轴的对称点,坐标为(-3,0),即是A点,设过A、C的直线为y=kx+b,则
,所以C点的坐标(0,-3);P为l上的一动点,当△PBC的周长=PB+PC+BC,因为BC的长度一定,所以要使△PBC的周长最小,即PB+PC最小,作点B关于对称轴的对称点,坐标为(-3,0),即是A点,设过A、C的直线为y=kx+b,则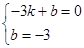
解得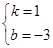 ,所以过点A、C的直线为y=x-3,则P点即为直线为y=x-3与对称轴的交点,解得
,所以过点A、C的直线为y=x-3,则P点即为直线为y=x-3与对称轴的交点,解得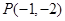
(3)存在,)直线l为x=-1,它与X轴的交点为N(-1,0),由(2)知B点的坐标(1,0),所以它们两点是关于原点对称,此时这三点构成了等腰三角形,M点即为对称轴与X轴的交点,所以M的坐标(-1,0);当△MBC是等腰三角形,并以BC为△MBC的底边,设M的坐标为(-1,y);此时需满足MB=MC,而MB=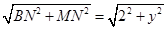 ,MC=
,MC=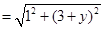 ,解得y=-1,y=
,解得y=-1,y=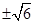 ,所以,当y=-1时M的坐标为
,所以,当y=-1时M的坐标为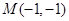 ,当y=
,当y=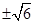 ,M的坐标为
,M的坐标为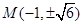 ;综上所述满足条件的M的坐标为
;综上所述满足条件的M的坐标为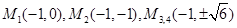
考点:抛物线
点评:本题考查抛物线,要求考生掌握抛物线的性质,会用待定系数法求抛物线的解析式,会求抛物线与坐标轴的交点坐标,以及对称轴


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线的顶点A在y轴上,坐标A(0,1)矩形CDEF的顶点C、F在抛物线上,D、E在x轴上,CF交y轴于点B(0,2),S矩形CDEF=8
如图,已知抛物线的顶点A在y轴上,坐标A(0,1)矩形CDEF的顶点C、F在抛物线上,D、E在x轴上,CF交y轴于点B(0,2),S矩形CDEF=8查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com