
【题目】如图,△ABC中,AB=AC=18,BC=12,正方形DEFG的顶点E,F在△ABC内,顶点D,G分别在AB,AC上,AD=AG,DG=6,则点F到BC的距离为( ) 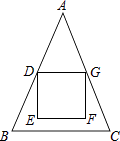
A.1
B.2
C.12 ![]() ﹣6
﹣6
D.6 ![]() ﹣6
﹣6
【答案】D
【解析】解:过点A作AM⊥BC于点M,交DG于点N,延长GF交BC于点H, ∵AB=AC,AD=AG,
∴AD:AB=AG:AC,
∵∠BAC=∠DAG,
∴△ADG∽△ABC,
∴∠ADG=∠B,
∴DG∥BC,
∵四边形DEFG是正方形,
∴FG⊥DG,
∴FH⊥BC,AN⊥DG,
∵AB=AC=18,BC=12,
∴BM= ![]() BC=6,
BC=6,
∴AM= ![]() =12
=12 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴AN=6 ![]() ,
,
∴MN=AM﹣AN=6 ![]() ,
,
∴FH=MN﹣GF=6 ![]() ﹣6.
﹣6.
故选:D.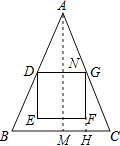
【考点精析】本题主要考查了等腰三角形的性质和勾股定理的概念的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,已知第一象限内的点A在反比例函数y= ![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y= ![]() 的图象上,且OA⊥OB,cosA=
的图象上,且OA⊥OB,cosA= ![]() ,则k的值为( )
,则k的值为( )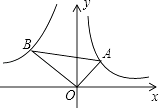
A.﹣3
B.﹣4
C.﹣ ![]()
D.﹣2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
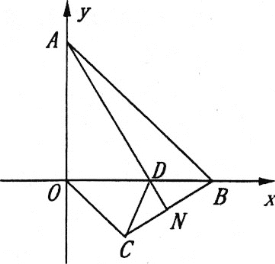
【题目】在平面直角坐标系xOy中,直线AB交y轴于A点,交X轴于B点,A(0,6),B(6,0).点D是线段BO上一点,BN⊥AD交AD的延长线于点N.
(1)如图,若OM∥BN交AD于点M.点O作0G⊥BN,交BN的延长线于点G,求证:AM=BG

(2)如图,若∠ADO=67.5°,OM∥BN交AD于点M,交AB于点Q,求![]() 的值.
的值.
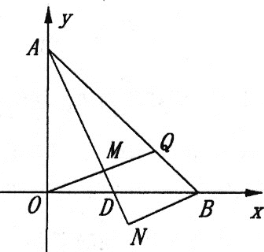
(3)如图,若OC∥AB交BN的延长线于点C.请证明:∠CDN+2∠BDN=180°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
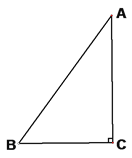
(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
![]() 在图中画出与
在图中画出与![]() 关于直线l成轴对称的
关于直线l成轴对称的![]() ;
;
![]() 三角形ABC的面积为______;
三角形ABC的面积为______;
![]() 以AC为边作与
以AC为边作与![]() 全等的三角形,则可作出______个三角形与
全等的三角形,则可作出______个三角形与![]() 全等;
全等;
![]() 在直线l上找一点P,使
在直线l上找一点P,使![]() 的长最短.
的长最短.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有x个黑球和y个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,它是黑球的概率是 ![]() ;若往盒中再放进1个黑球,这时取得黑球的概率变为
;若往盒中再放进1个黑球,这时取得黑球的概率变为 ![]() .
.
(1)填空:x= , y=;
(2)小王和小林利用x个黑球和y个白球进行摸球游戏.约定:从盒中随机摸取一个,接着从剩下的球中再随机摸取一个,若两球颜色相同则小王胜,若颜色不同则小林胜.求两个人获胜的概率各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(1,6)和点M(m,n)都在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,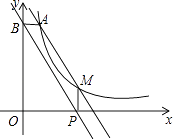
(1)k的值为;
(2)当m=3,求直线AM的解析式;
(3)当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com