
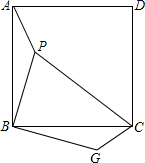
 如图,已知P是正方形ABCD内一点,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.
如图,已知P是正方形ABCD内一点,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.分析 (1)因为将△ABP按顺时针方向旋转使点A与点C重合,即旋转了90°,利用面积差可得边PA所扫过区域的面积=S=S扇形BAC+S△CBG-S△ABP-S扇形BPG,代入可得结论;
(2)先利用勾股定理得PG=$\sqrt{2}$,根据勾股定理的逆定理可得:△PGC是等腰直角三角形.
解答 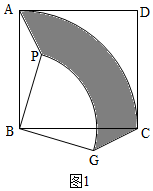 解:(1)如图1,由旋转得:∠PBG=∠ABC=90°,BG=PB=b,
解:(1)如图1,由旋转得:∠PBG=∠ABC=90°,BG=PB=b,
△ABP≌△CBG,
∴S=S扇形BAC+S△CBG-S△ABP-S扇形BPG,
=$\frac{90π•{a}^{2}}{360}$-$\frac{90π•{b}^{2}}{360}$,
=$\frac{({a}^{2}-{b}^{2})π}{4}$,
故答案为:$\frac{({a}^{2}-{b}^{2})π}{4}$;
(2)如图2,△PGC是等腰直角三角形,
理由是:∵∠PBG=90°,PB=BG=1,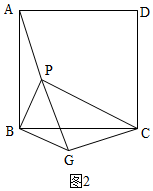
∴△PBG是等腰直角三角形,
∴PG=$\sqrt{2}$,
△PGC中,PC=2,CG=$\sqrt{2}$,
∴PC2=PG2+CG2,
∴△PGC是直角三角形,
∵CG=PG,
∴△PGC是等腰直角三角形.
点评 本题考查了正方形的性质、旋转的性质、勾股定理及其逆定理、等腰直角三角形的性质和判定、扇形的面积,明确旋转前后的边和角对应相等,并熟练掌握扇形面积的计算公式.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3种 | B. | 4种 | C. | 5种 | D. | 6种 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
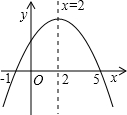 已知函数y=ax2+bx+c 的图象如图所示,则下列判断不正确的是( )
已知函数y=ax2+bx+c 的图象如图所示,则下列判断不正确的是( )| A. | 关于x的方程ax2+bx+c=0的根是x1=-1,x2=5 | |
| B. | a-b+c>0 | |
| C. | b=-4a | |
| D. | ac<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
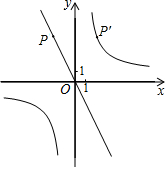 如图,已知直线y=-2x,经过点P(-2,a),点P关于y轴的对称点P′在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.
如图,已知直线y=-2x,经过点P(-2,a),点P关于y轴的对称点P′在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
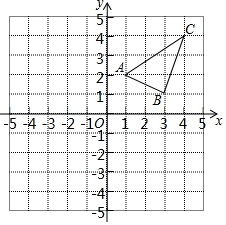 学习完轴对称后,黑板展示区出了一道作图题(不写作法,保留作图痕迹).
学习完轴对称后,黑板展示区出了一道作图题(不写作法,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com