
【题目】书籍是人类进步的阶梯,联合国教科文组织把每年的4月23日确定为“世界读书日”,某校为了了解该校学生一个学期阅读课外书籍的情况,在全校范围内随机对100名学生进行了问卷调查,根据调查的结果,绘制了统计图表的一部分:一个学期平均一天阅读课外书籍所有时间统计表
时间(分钟) | 20 | 40 | 60 | 80 | 100 | 120 |
人数 | 43 | 31 | 15 | 5 | 4 | 2 |
请你根据以上信息解答下列问题:
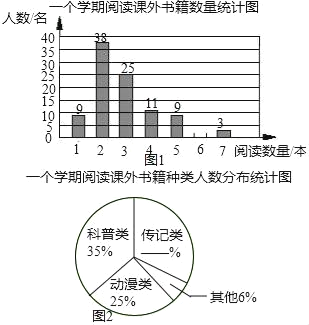
(1)补全图1、图2;
(2)这100名学生一个学期平均每人阅读课外书籍多少本?若该校共有1200名学生,请你估计这个学校学生一个学期阅读课外书籍共多少本?
(3)根据统计表,求一个学期平均一天阅读课外书籍所用时间的众数和中位数.
【答案】(1)见解析;(2)估计这个学校学生一个学期阅读课外书籍共3600本;(3)众数为20分钟,中位数为40分钟
【解析】
(1)根据条形统计图和扇形统计图,求出阅读6本的人数和阅读传记类的人数的比例,补全图1,图2;
(2)根据平均数的概念求出一个学期平均每人阅读课外书的本数,再求出这个学校学生一个学期阅读课外书籍的总数.
(3)依据统计表中的数据可得,一个学期平均一天阅读课外书籍所用时间为20分钟的人数最多,中位数为落在第二组中.
解:(1)阅读6本的人数=100﹣9﹣38﹣25﹣11﹣9﹣3=5人,
阅读传记类的人数的比例=1﹣35%﹣6%﹣25%=34%,
补全统计图如下:
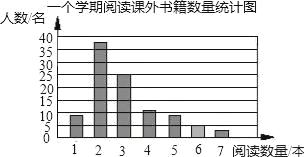
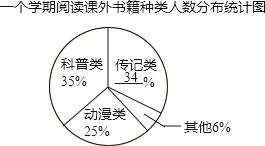
(2)这100名学生一个学期平均每人阅读课外书籍为:![]() (9×1+38×2+25×3+11×4+9×5+5×6+3×7)=3(本),
(9×1+38×2+25×3+11×4+9×5+5×6+3×7)=3(本),
即这100名学生一个学期平均每人阅读课外书籍3本,
∴1200×3=3600(本),
估计这个学校学生一个学期阅读课外书籍共3600本;
(3)由统计表可得,众数为20分钟,中位数为40分钟.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的延长线上的一动点,连接
的延长线上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,与线段
,与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 是平行四边形.
是平行四边形.
![]() 若
若![]() ,
,![]() ,则在点
,则在点![]() 的运动过程中:
的运动过程中:
①当![]() ________时,四边形
________时,四边形![]() 是矩形,试说明理由;
是矩形,试说明理由;
②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?
(精确到米,参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin67°≈
,sin67°≈![]() ,tan67°≈
,tan67°≈![]() )
)
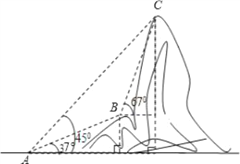
查看答案和解析>>
科目:初中数学 来源: 题型:
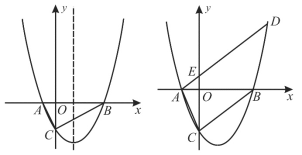
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(A点在B点的左边),与
两点(A点在B点的左边),与![]() 轴交于点
轴交于点![]() .
.
(1)如图1,若△ABC为直角三角形,求![]() 的值;
的值;
(2)如图1,在(1)的条件下,点![]() 在抛物线上,点
在抛物线上,点![]() 在抛物线的对称轴上,若以
在抛物线的对称轴上,若以![]() 为边,以点
为边,以点![]() 、
、![]() 、
、![]() 、Q为顶点的四边形是平行四边形,求
、Q为顶点的四边形是平行四边形,求![]() 点的坐标;
点的坐标;
(3)如图2,过点![]() 作直线
作直线![]() 的平行线交抛物线于另一点
的平行线交抛物线于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() ﹕
﹕![]() =1﹕4. 求
=1﹕4. 求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AC=9,S△ABC=![]() ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
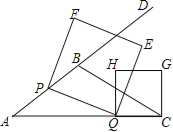
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+a与x轴交于点A(4,0),与y轴交于点B,抛物线y=
x+a与x轴交于点A(4,0),与y轴交于点B,抛物线y=![]() x2+bx+c经过点A,B.点M(m,0)为x轴上一动点,过点M且垂直于x轴的直线分别交直线AB及抛物线于点P,N.
x2+bx+c经过点A,B.点M(m,0)为x轴上一动点,过点M且垂直于x轴的直线分别交直线AB及抛物线于点P,N.
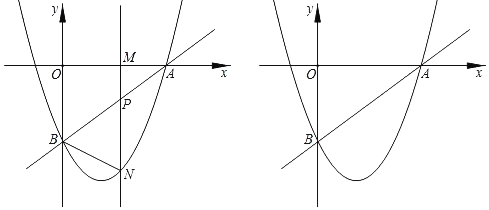
(1)填空:点B的坐标为 ,抛物线的解析式为 ;
(2)当点M在线段OA上运动时(不与点O,A重合),
①当m为何值时,线段PN最大值,并求出PN的最大值;②求出使△BPN为直角三角形时m的值;
(3)若抛物线上有且只有三个点N到直线AB的距离是h,请直接写出此时由点O,B,N,P构成的四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个小球沿着足够长的光滑斜面向上滚动,它的速度与时间满足一次函数关系,其部分数据如下表:

(1) 求小球的速度v与时间t的关系.
(2)小球在运动过程中,离出发点的距离S与v的关系满足![]() ,求S与t的关系式,并求出小球经过多长时间距离出发点32m?
,求S与t的关系式,并求出小球经过多长时间距离出发点32m?
(3)求时间为多少时小球离出发点最远,最远距离为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知![]() ,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程_____.
,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB 为圆O的直径, PQ切圆O于T , AC⊥PQ于C ,交圆O于 D .
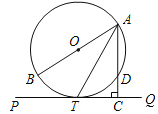
(1)求证: AT 平分∠BAC ;
(2)若 AD =2 , TC=![]() ,求圆O的半径.
,求圆O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com