
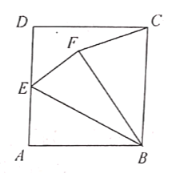
【题目】如图,正方形![]() 的边长为2,点
的边长为2,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为
的对应点为![]() .连接CF,则
.连接CF,则![]() 的长为( )
的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
连接AF交BE于点O,过点F作MN⊥AB,由勾股定理可求BE的长,由三角形面积公式可求AO的长,由折叠的性质可得AO=OH= ![]() ,AB=BF=2,由勾股定理可求BN,FN的长,由矩形的性质可求FM,MC的长,由勾股定理可求CF的长.
,AB=BF=2,由勾股定理可求BN,FN的长,由矩形的性质可求FM,MC的长,由勾股定理可求CF的长.
解:如图,连接AF交BE于点O,过点F作MN⊥AB,

∵AB∥CD,MN⊥AB,
∴MN⊥CD,
∵AB=2=AD,点E是AD中点,
∴AE=1,
∴EB=![]() ,
,
∵S△ABE=![]() ×AB×AE=
×AB×AE=![]() ×BE×AO,
×BE×AO,
∴2×1=![]() AO,
AO,
∴AO=![]() ,
,
∵将△ABE沿BE折叠,点A的对应点为F,
∴AO=OH=![]() ,AB=BF=2,
,AB=BF=2,
∴AF=![]() ,
,
∵AF2-AN2=FN2,BF2-BN2=FN2,
∴AF2-AN2=BF2-BN2,
∴![]() -(2-BN)2=4-BN2,
-(2-BN)2=4-BN2,
∴BN=![]() ,
,
∴FN=![]() ,
,
∵MN⊥AB,MN⊥CD,∠DCB=90°,
∴四边形MNBC是矩形,
∴BN=MC=![]() ,BC=MN=2,
,BC=MN=2,
∴MF=![]() ,
,
∴CF=![]() .
.
故选:D.


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
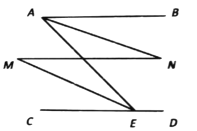
【题目】已知如图,![]() ,
,![]() .
.
求证:![]()
证明:因为![]() (已知)
(已知)
所以![]() (_______)
(_______)
所以![]() __________.(两直线平行,内错角相等)
__________.(两直线平行,内错角相等)
因为![]() .(已知)
.(已知)
所以![]() __________.(_______)
__________.(_______)
所以![]() .(_______)
.(_______)
所以![]() .(等式性质1)
.(等式性质1)
即![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
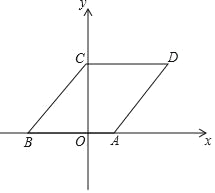
【题目】如图,在平面直角坐标系中,菱形ABCD的边AB在x轴上,点B坐标(﹣3,0),点C在y轴正半轴上,且sin∠CBO=![]() ,点P从原点O出发,以每秒一个单位长度的速度沿x轴正方向移动,移动时间为t(0≤t≤5)秒,过点P作平行于y轴的直线l,直线l扫过四边形OCDA的面积为S.
,点P从原点O出发,以每秒一个单位长度的速度沿x轴正方向移动,移动时间为t(0≤t≤5)秒,过点P作平行于y轴的直线l,直线l扫过四边形OCDA的面积为S.
(1)求点D坐标.
(2)求S关于t的函数关系式.
(3)在直线l移动过程中,l上是否存在一点Q,使以B、C、Q为顶点的三角形是等腰直角三角形?若存在,直接写出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需要粉刷一些相同的房间,经调查3名师傅一天粉刷8个房间,还剩40m2刷不完;5名徒弟一天可以粉刷9个房间;每名师傅比徒弟一天多刷30m2的墙面。
(1)求每个房间需要粉刷的面积;
(2)该公司现有36个这样的房间需要粉刷,若只聘请1名师傅和2名徒弟一起粉刷,需要几天完成?
(3)若来该公司应聘的有3名师傅和10名徒弟,每名师傅和每名徒弟每天的工资分别是240元和200元,该公司要求这36个房间要在2天内粉刷完成,问人工费最低是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某公司员工的年收入情况,随机抽查了公司部分员工年收入情况并绘制如图所示统计图.
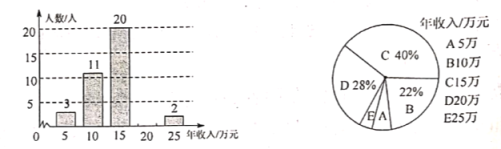
(1)请按图中数据补全条形图;
(2)由图可知员工年收入的中位数是 ,众数是 ;
(3)估计该公司员工人均年收入约为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“※”定义一种新运算:对于任意有理数a和b,规定a※b=ab2+2ab+a.
如:1※2=1×22+2×1×2+1=9
(1)(﹣2)※3= ;
(2)若![]() ※3=16,求a的值;
※3=16,求a的值;
(3)若2※x=m,(![]() x)※3=n(其中x为有理数),试比较m,n的大小.
x)※3=n(其中x为有理数),试比较m,n的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.

(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课堂上李老师给出了一道整式求值的题目,李老师把要求的整式(7a3-6a3b+3a2b)-(-3a3-6a3b+3a2b+10a3-3)写完后,让王泓同学顺便给出一组![]() 的值,老师自己说答案,当王泓说完:“
的值,老师自己说答案,当王泓说完:“![]() ”后,李老师不假思索,立刻就说出答案:“3”。同学们觉得不可思议,李老师用坚定的口吻说:“这个答案准确无误。”聪明的同学们,你能说出其中的道理吗?
”后,李老师不假思索,立刻就说出答案:“3”。同学们觉得不可思议,李老师用坚定的口吻说:“这个答案准确无误。”聪明的同学们,你能说出其中的道理吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com