练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．一队学生从学校步行去博物馆，他们以5km/h的速度行进24min后，一名教师骑自行车以15km/h的速度按原路追赶学生队伍．这名教师从出发到途中与学生队伍会合用了多少时间？

    分析 根据教师的路程等于学生的路程，可得方程，根据解方程，可得答案．

    解答 解：设用了x小时这名教师追赶上学生队伍，由题意，得
    24分=0.4小时，则学生行了0.4×5千米，
    所以15x-5x=0.4×5
    10x=2
    x=0.2
    0.2小时=12分钟，
    答：这名教师从出发到途中与学生队伍会合共用了18分钟．

    点评 本题考查了一元一次方程的应用，教师的路程等于学生的路程得出方程是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．郑州市北环彩虹桥在上下班高峰期经常堵车，交通管理部门为了解交通拥堵情况，进行了统计分析，桥上的车流速度v（km/h）关于车流密度x（辆/km）的函数图象如图所示．
    （1）请直接写出v与x之间的函数关系式；
    （2）在交通高峰时段，为使大桥上的车流速度大于30km/h且小于50km/h，应控制大桥上的车流密度在什么范围内？
    （3）车流量y（辆/h）是单位时间内通过桥上某观测点的车辆数，即车流量=车流速度×车流密度，求大桥上车流量的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列函数是一次函数但不是正比例函数的是（　　）
    A．y=-$\frac{1}{x}$B．y=x2C．y=xD．y=$\frac{x+1}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．下列各式中，是分式的是（　　）
    A．$\frac{{x}^{2}+1}{2}$B．$\frac{3xy}{π}$C．$\frac{3}{xy}$D．$\frac{m-n}{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．化简或计算：
    （1）$\frac{{a}^{2}bc}{ac}$；
    （2）$\frac{{x}^{2}-1}{{x}^{2}-x}$；
    （3）（$\frac{1}{x-2}$-1）÷$\frac{3-x}{{x}^{2}-4}$；
    （4）（$\frac{-a}{b}$）2÷$\frac{（2a）^{2}}{5b}$+$\frac{{a}^{2}}{{b}^{2}}$•$\frac{b}{2a}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

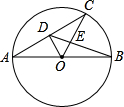    6．如图，AB为⊙O的直径，AC为弦，OD⊥AC于点D，BD交OC于点E，若AC=4，AB=5，则BE=$\frac{2\sqrt{13}}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知等式y=kx+b，当x=2时，y=-3，当x=-1时，y=3，求当x=-2时，y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

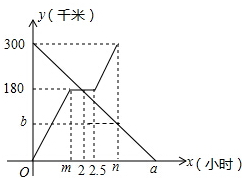    10．甲、乙两车分别从A，B两地同时出发相向而行．并以各自的速度匀速行驶，甲车途经C地时休息1小时，然后按原速度继续前进到达B地；乙车从B地直接到达A地，如图是甲、乙两车和B地的距离y（千米）与甲车出发时间x（小时）的函数图象．
    （1）直接写出m，n，a，b的值；m=1.5；n=3.5；a=5；b=90．
    （2）求出甲车与B地的距离y（千米）与甲车出发时间x（小时）的函数关系式（写出自变量x的取值范围）；
    （3）当两车相距120千米时，乙车行驶了多长时间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

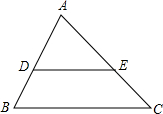    11．如图，已知点D、E在△ABC的边上，DE∥BC，∠B=60°，∠AED=40°，则∠A的度数为（　　）
    A．70°B．80°C．90°D．100°

    查看答案和解析>>

    同步练习册答案